不等式在生产实践和相关学科的学习中应用广泛,又是学习高等数学的工具,所以不等式是高考数学命题的重点.不等式的性质的考查常与函数的性质等结合在一起,一般多以选择题的形式出现,有时与充要条件的知识结合起来.
例1、(黄冈)已知实数a,b,c满足条件: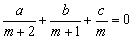 ,其中m是正数,对于f(x)=ax2+bx+c. ,其中m是正数,对于f(x)=ax2+bx+c.
(1)求证: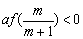 ; ;
(2)当a为何值时,方程f(x)=0在(0,1)内有解?
分析:本题利用不等式的基本性质,充分体现了函数、方程与不等式之间的关系。
解:

∴m>0,∴ . .
(2)f(0)=c,f(1)=a+b+c,当a>0时,由(1)知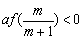 ,∴ ,∴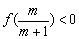 . .
若c>0,f(0)=c>0,∴方程f(x)=0在(0,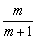 )内有解. )内有解.
若c≤0,f(1)= a+b+c=a+(m-1)·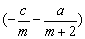 +c= +c=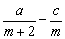 >0, >0,
∴方程f(x)=0在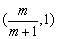 内有解. 内有解.
当a<0时,同理可证.
由(1)知a≠0,故当a≠0时,方程f(x)=0在(0,1)内有解.
应用问题与不等式的结合考查在高考中非常多见,尤其是运用重要不等式,求最值的题型.
例2、设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为λ(λ<1),画面的上、下各留8cm的空白,左、右各留5cm的空白.怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?(全国高考题)
分析:
先根据题意画出草图,设画面的宽为自变量x(cm),将所用纸张面积表示成x的函数,再求函数的最小值.

解:如图所示,设画面的宽为xcm,则画面的高为 ,设纸张面积为Scm2. ,设纸张面积为Scm2.
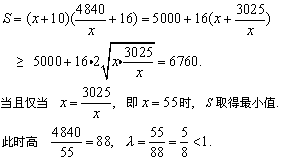
答:画面高为88cm,宽为55cm时,能使所用纸张面积最小.
例3、(全国·理·文)甲、乙两地相距S千米,汽车从甲地匀速行驶到乙地,速度不得超过c千米/时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/时)的平方成正比,比例系数为b;固定部分为a元.
(1)把全程运输成本y(元)表示为速度v(千米/时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
分析:根据题意建立函数关系式,然后运用不等式的性质求最值.
解:
(1)依题意知汽车从甲地匀速行驶到乙地所用时间为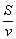 ,全程运输成本为 ,全程运输成本为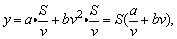
故所求函数及其定义域为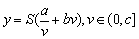 . .
(2)依题意知S,a,b,v都为正数,故有

因为c-v≥0,且a>bc2,故有a-bcv≥a-bc2>0,
所以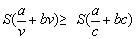 ,且仅当v=c时等号成立, ,且仅当v=c时等号成立,
也即当v=c时,全程运输成本y最小.
综上知,为使全程运输成本y最小,当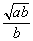 ≤c时行驶速度应为v= ≤c时行驶速度应为v=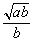 ; ;
当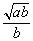 >c时行驶速度应为v=c. >c时行驶速度应为v=c.
小结:
与不等式有关的应用问题,在用重要不等式求最值时,应注意“正、定、等”三个字,即研究的对象为正数,积或和为定值,相等时取最小值或最大值.
|