1、课本P12上例2:“已知a,b,m都是正数,并且a<b,求证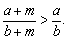 ” ”
为了应用上的方便,可将不等式作出推广:即当0<a≤b,且m≥0时,有 ,其中等号当且仅当a=b或m=0成立. ,其中等号当且仅当a=b或m=0成立.
下面我们看看此不等式的应用.
例、设a>b>m>0,求证:
分析:运用以上不等式及余弦函数的单调性去证明.
证明:由a>b>m>0,有

又y=cosx在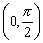 内是减函数,从而有 内是减函数,从而有
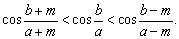
下面请同学们运用此不等式来证明下题:
设a,b为实数,求证: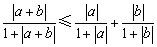 . .
提示:取m=|a|+|b|-|a+b|,可见m≥0, 于是
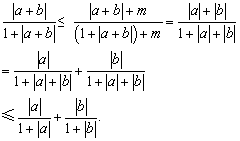
2、柯西不等式是一个很重要的不等式,它的形式如下:对于任意实数ai,bi(i=1,2,…,n),有(a1b1+a2b2+…+anbn)2≤(a12+a22+…+an2)(b12+b22+…+bn2),其中当且仅当ai=kbi,即ai与bi(i=1,2,…,n)成比例时取等号,对于这个不等式,我们可以采取构造函数法证之.
证明:
显见,对x,ai,bi的一切实数值(不妨设bi(i=1,2,…,n)不全为零,否则命题显然成立.),多项式
(b1x-a1)2+(b2x-a2)2+…+(bnx-an)2
恒不为负,即对于一切实数x,有
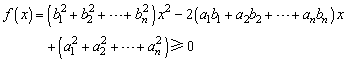
从而方程f(x)=0的判别式
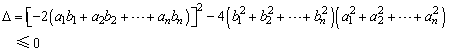
由此即得
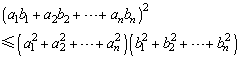
其中当且仅当方程f(x)=0有二重根x=k时取等号.
于是可由 
推得,当且仅当 bik-ai=0,即ai=kbi(i=1,2,…,n)时取等号.
现在同学们可尝试用柯西不等式证明下题:
如果a1,a2,…,an为实数,那么:

提示:

|