随着课程的改革,思维能力放在四大能力之首,而不等式知识又是较好的考查代数推理的章节,也就使得它成为高考的热点,不等式的证明也在九十年代后期达到了考查的高潮.
在不等式证明中着重要求掌握不等式证明的几种常见方法:比较法、分析法和综合法,其它不作为重点,但其它方法如反证法、换元法、函数单调性法等等是高中数学和高等数学都常用的数学思维方法,因此,也是考察学生能力的内容之一.“正难则反”适用反证法,求参数的取值范围一般用判别式法,而放缩法贯穿于每一证明的过程中.总之,不等式的证明作为高考命题的热点,要重视思想方法的掌握与运用.
试题一般考查的思想主要有:分类讨论思想,等价转化思想,函数与方程思想,数形结合思想.试题考查的能力主要是:运算能力,逻辑思维能力和分析问题,解决问题的能力.试题考查的主要技能和方法是:比较法、综合法证明不等式,试题上的立意年年有创新.
【例1】(全国高考试题)已知f(x)=tanx, ,若 ,若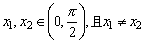 , ,
证明: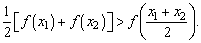
【分析】本题主要考查的是函数的性质,均值不等式及推理论证的能力.
【证明】
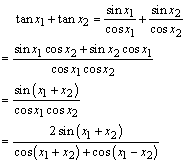
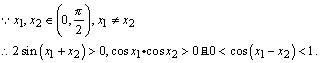
从而有:0<cos(x1+x2)+cos(x1-x2)<1+cos(x1+x2),由此得
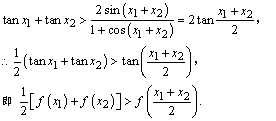
【例2】(全国高考题)设{an}是由正整数组成的等比数列,Sn是其前n项和.
(1)证明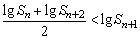 ; ;
(2)是否存在常数c>0,使得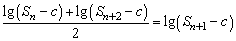 成立?并证明你的结论. 成立?并证明你的结论.
【分析】 本题主要考查等比数列,对数,不等式等基础知识,推理能力以及分析问题和解决问题的能力.
【解答】
(1)证明:设{an}的公比为q,由题设知a1>0,q>0,
1)当q=1时,Sn=na,从而
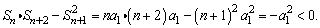
2)当q≠1时,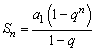 ,从而 ,从而
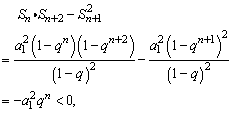
由1)和2)得:
又由对数的单调性,知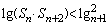 , ,
即 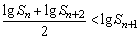 . .
(2)假设存在常数c>0,使
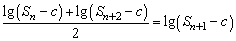 ,则有 ,则有

由④得 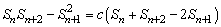 ,⑤ ,⑤
根据平均值不等式及①、②、③、④知
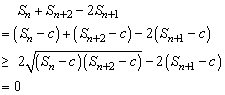
∵ c>0,故⑤式右端非负,而由(1)知⑤式左端小于零,矛盾.
故不存在常数c>0,使
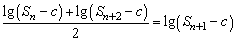 . .
|