1、已知映射f:A→B,其中A=B=R,对应法则f:y=-x2+2x,对于实数k∈B,在集合A中不存在原象,则k的取值范围是( )
A.k>1 B.k≥1
C.k<1 D.k≤1
2、已知0<|a|<|b|<|c|,b<0,且满足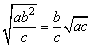 ,则下列不等式中成立的是( )
,则下列不等式中成立的是( )
A.c<b<a B.a<b<c
C.b<a<c D.b<c<a
3、已知0<x< ,下列各式中正确的是( )
,下列各式中正确的是( )
A.2x>21-x
B.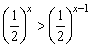
C.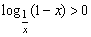 D.logx(1-x)<1
D.logx(1-x)<1
4、设a>b>0,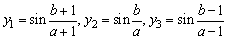 ,则y1,y2,y3的大小关系是( )
,则y1,y2,y3的大小关系是( )
A.y1< y2< y3 B.y2< y1< y3
C.y3< y2< y1 D.y2<y3<y1
5、不等式(1+x)(1-|x|)>0的解集是( )
A.{x|0≤x<1} B.{x|x<0且x≠-1}
C.{x|-1<x<1} D.{x|x<1且x≠-1}
6、设a,b∈R,现给出下列五个条件:
①a+b=2; ②a+b>2; ③a2+b2>2;
④ab>1; ⑤logab<0,
其中能推出:“a,b中至少有一个大于1”的条件为( )
A.②③④ B.②③④⑤
C.①②③⑤ D.②⑤
7、若ε>0,命题甲:“a,b为实数,且|a-b|<2ε”;命题乙:“a,b为实数,满足|a-2|<ε且|b-2|<ε”,则( )
A.甲是乙的充要条件
B.甲是乙的充分非必要条件
C.甲是乙的必要非充分条件
D.甲是乙的非充分非必要条件
8、若关于x的不等式:x2-ax-6a<0有解且解区间长度不超过5个单位长,则a的取值范围是( )
A.-25≤a≤1 B.a≤-25或a≥1
C.-25≤a<0或1≤a<24 D.-25≤a<-24或0<a≤1
9、若a,b∈R,且2a+b=1,则S=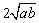 -4a2-b2的最大值为( )
-4a2-b2的最大值为( )
A.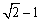 B.
B.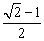
C. D.
D.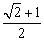
10、已知不等式组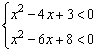 的解集是不等式2x2-9x+a<0的解集的子集,则实数a的取值范围是( )
的解集是不等式2x2-9x+a<0的解集的子集,则实数a的取值范围是( )
A.(9,+∞) B.{9}
C.(-∞,9] D.(0,9]
11、已知f(x)是定义在(-3,0)∪(0,3)上的奇函数,当0<x<3时,f(x)的图像如图所示,那么不等式f(x)·cosx<0的解集为( )