|
一、选择题
1、给出下列命题:
①有一条侧棱与底面两边垂直的棱柱是直棱柱;
②底面为正多边形的棱柱为正棱柱;
③顶点在底面上的射影到底面各顶点的距离相等的棱锥是正棱锥;
④A、B为球面上相异的两点,则通过A、B的大圆有且仅有一个.
其中正确命题的个数是( )
A.3个 B.2个
C.1个 D.0个
2、在半径为5的球面上有两点A、B,若AB=6,则球心到A、B的截面的距离的最大值为( )
A.3 B.4
C.6 D.8
3、地球半径为R,则北纬60°纬线圈的长是( )
A.R B.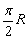
C. D.πR D.πR
4、设A、B、C、D是球面上的四个点,且在同一平面内,AB=BC=CD=DA=3,球心到该平面的距离是球半径的一半,则球的体积是( )

5、已知正四面体ABCD的表面积为S,其四个面的中心分别为E、F、G、H.设四面体EFGH的表面积为T,则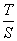 等于( ) 等于( )
A. B. B.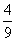
C. D. D.
6、一个四面体的所有棱长都为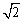 ,四个顶点在同一球面上,则此球的表面积为( ) ,四个顶点在同一球面上,则此球的表面积为( )
A.3π B.4π
C. D.6π D.6π
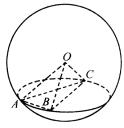
7、如图,A、B、C是表面积为48π的球面上三点,AB=2,BC=4,∠ABC=60°,O为球心,则直线OA与截面ABC所成的角是( )

8、正方体的棱长为a,连接正方体相邻各面的中心构成的几何体的体积是( )

9、过四面体共一个顶点的三条棱的中点可以确定一个截面,这样的截面共有四个,用这四个截面截去四个小四棱锥后剩下的几何体的表面积与原四面体的表面积之比等于( )
A.2︰3 B.1︰2
C.1︰3 D.1︰4
10、已知A、B、C、D为同一球面上的四点,且连接每两点间的线段长都等于2,则球心O到平面BCD的距离等于( )

11、长方体ABCD-A1B1C1D1中,AB=3,BC=2,AA1=1,一蚂蚁从点A沿其表面爬到C1点的最短路程为( )

12、已知高为3的直棱锥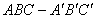 的底面是边长为1的正三角形(如图所示),则三棱锥 的底面是边长为1的正三角形(如图所示),则三棱锥 的体积为( ) 的体积为( )
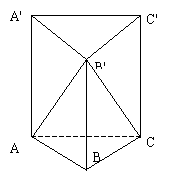
A.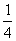 B. B.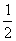
C.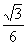 D. D.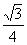
二、填空题
13、正二十面体棱长为a,则其各面面积之和为_________.
14、已知正方体的棱长为a,则此正方体的各面中心为顶点的多面体为_________,此多面体的对角线长为_________.
15、半径为10cm的球被两个平行平面所截,截得的截面面积分别为36πcm2,64πcm2,则这两个平面间的距离是_____________.
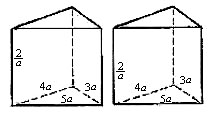
16、有两个相同的直三棱柱,高为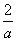 ,底面三角形的三边长分别为 ,底面三角形的三边长分别为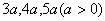 。用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,表面积最小的是一个四棱柱,则 。用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,表面积最小的是一个四棱柱,则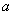 的取值范围是__________. 的取值范围是__________.
[答案] 三、解答题
17、求证:过球内一定点所引的弦被该点分成的两部分的积是定值.
[答案]
18、已知三棱锥A-BCD中,CD=4,其余各棱长都是3.求此三棱锥的体积.
[答案]
19、把半径为2的四个小球垒成两层放在桌面上,两两相切.求上层的最高点离桌面的距离.
[答案]
20、已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4.求球面面积与球的体积.
[答案]
21、已知正三棱锥的高及底面边长都是a.求它的外接球和内切球的半径.
[答案]
22、某商人要从北京(北纬40°,东经120°)乘飞机去南非首都约翰内斯堡(南纬30°,东经30°)处理紧急商务,现有两条航线可供选择:甲航线,从北京沿纬度弧向西飞到希腊首都雅典(北纬40°,东经30°),然后向南飞到目的地;乙航线,从北京向南飞到澳大利亚的佩思(南纬30°,东经120°),然后沿纬度弧向西飞到目的地.若这两条航线的飞机航速均为1000km/h,中途转航需要1h.在正常情况下,求该商人选择的最短路程所需的时间(地球半径约为6370km).
[答案]
|