例1、（福州市）由0，2，5，6，7，8六个数字组成没有重复数字的数，
（1）求四位数的个数；
（2）设四位奇数有a个，四位偶数有b个，求a－b的值；
（3）设5的倍数的三位数有x个，求x；
（4）求是25的倍数的四位数的个数；
（5）将所有的四位数从小到大排成数列{an}，设am=5 607，求m；
（6）在（5）中的数列{an}中，求a128．
解析：
1）首位不能是0，有5种排法，其余位数上随意排，共有
（2）奇数的个位数只能是5或7，首位不能是0，共有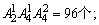
即a=96，偶数的个位可以是0，2，6，8之一，但0不能作首位，0在个位的有
0不在个位的有
共有204个，即b=204，∴a－b=－108；
（3）是5的倍数的个位数只能是0或5，共有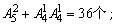
（4）小于5607的四位数具有的形式为2×××，50××，52××和5602的数，
共有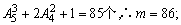
（5）形如2×××，50×××的数各有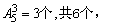
接下来的是6072和6075，∴a128=6075．
例2、（新教材）如图所示，一个地区分为5个行政区，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有_____种（用数字作答）．
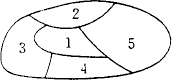
解析：
第一步：染1区，有4种方法；
第二步：染2区，有3种方法；
第三步：染3区，有2种方法；
第四步：染4区，当4区与2区同色时，第四步有1种方法，此时第五步有2种方法；当4区与2区不同色时，第四步也是1种方法，此时第五步是1种方法.
根据分步计数原理，不是着色方法有4×3×2×(1×2＋1×1)＝72（种）
