高考对排列内容的考查，多为选择、填空题．一般以实际应用题形式出现，这是因为排列的应用性概念强，并充满思辨性和解法的多样性，符合高考选择题的特点，易于考查学生的能力，此类题主要有附加条件的排列问题，多数只有一个附加条件，且以学生熟悉的数字问题或排队问题为主．
因此，本节内容应立足基础知识和基本方法的学习，恰当选取典型例题，构建思维模式，造就思维依托和思维的合理定势，如对排列应用题可用①某元素排在某位上；②某元素不排在某位上；③某几个元素排在一起；④某几个元素不得相邻；⑤某几个元素顺序一定等基本问题，加强思维的规范训练．
例1、（福州市）由0，2，5，6，7，8六个数字组成没有重复数字的数，
（1）求四位数的个数；
（2）设四位奇数有a个，四位偶数有b个，求a－b的值；
（3）设5的倍数的三位数有x个，求x；
（4）求是25的倍数的四位数的个数；
（5）将所有的四位数从小到大排成数列{an}，设am=5607，求m；
（6）在（5）中的数列{an}中，求a128．
解析：
（1）首位不能是0，有5种排法，其余位数上随意排，共有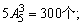
（2）奇数的个位数只能是5或7，首位不能是0，共有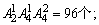
即a=96，偶数的个位可以是0，2，6，8之一，但0不能作首位，0在个位的有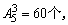
0不在个位的有
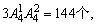共有204个，即b=204，∴a－b=－108；
（3）是5的倍数的个位数只能是0或5，共有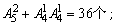
（4）小于5607的四位数具有的形式为2×××，50××，52××和5602的数，
共有
（5）形如2×××，50×××的数各有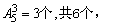
接下来的是6072和6075，∴a128=6075．
例2、（新教材）将3种作物种植在如图所示的5块试验田里，每一块种植一种作物且相邻的试验田不能种植同一作物，不同的种植方法共有______种（以数字作答）．
解析：
将5块试验田从左到右依次看作甲、乙、丙、丁、戊，3种作物依次看作A、B、C，则3种作物都可以种植在甲试验田里，由于相邻的试验田不能种植同一种作物，从而可知在乙试验田里只能有两种作物．同理，在丙、丁、戊试验田里也只能有两种作物可以种植．
由分步计数原理，不同的种植方法共有3×2×2×2=48种．
∴应填：48
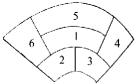
例3、（全国高考题）某城市中心广场建造一个花圃，花圃分为6个部分（如图），现要栽种4种不同颜色的花，每部分栽种1种且相邻部分不能栽种同样颜色的花，不同的栽法有_______种．
解析：
由于第1、2、3块两两相邻，我们先安排这三块，给第1、2、3块种花时分别有4、3、2种种法，所以共有4×3×2=24种不同种法．
下面给第4块种花，若第4块与第6块同色，只有一种种植方法，则第5块只有2种种法，若第4块与第2块同色时，共有2×1=2种种法．
若第4块与第6块不同色，但第4块与第2块同色，则第6块有2种种植的方案，而第5块只有1种种法，共有2种不同的种植方法．
若第4块与第6块不同色，但第4块与第2块不同色，则第6块有1种种法，则第5块也有一种不同种法，所以第4块与第6块不同色时，有1种种法．
综上共有24×(2＋2＋1)=120种不同的种植方法．
