排列问题往往与集合，立体几何相联系，且解法多样化，具有较强的综合能力．

例1、（全国）用1，2，3，4，5这五个数字，组成没有重复数字的三位数，其中偶数共有（　）

　A．24个　　　　　B．30个　　　　C．40个　　　　　　D．60个

解析一：（分类计算）

　　将符合条件的偶数分为两类，一类是2作个位数，共有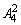个；另一类是4作个位数，也有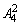个，因此符合条件的偶数共有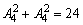个．

解析二：（分步计算）

　　先排个位数字，有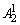种排法，再排十位和百位数字，有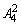种排法，根据分步计数原理，三位偶数应有.

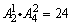解析三：（按概率算）

　　用1—5这5个数字可以组成没有重复数字的三位数共有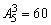 个，其中偶数占其中的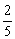，因此三位偶数共有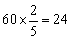个.

解析四：（利用选择项判断）

　　用1—5这5个数字可以组成没有重复数字的三位数共有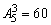 个.其中偶数少于奇数，因此偶数的个数应少于30个，四个选择项所提供的答案中，只有A符合条件．

　　∴应选A

例2、集合A、B的并集A∪B={a,b,c}，当A≠B时（A、B）与（B、A）视为不同的对，则这样的（A、B）对的个数有多少．

解析：

　　若A={A,B,C}，则满足题意的B有23个，即A的任意一个子集均可以为B，故此时的配对的个数是8．

　　若A={a,b}，则满足题意的B必含有c，这时B可以认为由{a,b}子集再加上元素c构成，此时的配对个数为22=4；同理若A={b,c}或A={a,c}时，则相应的配对个数也分别为4个；故当A中有2个元素时，配对个数为3×4=12个．

　　若A中有一个元素时，如A={a}时，则b∈B、c∈B，故B只有2种可能（a∈B或a），从而可知，配对个数为3×2=6.

　　若A=Ф（空集），则B={a,b,c}

　　综上所述，全部配对个数为8＋12＋6＋1=27.

例3、由四个不同的数字1，4，5，x(x≠0)组成没有重复数字的所有四位数的各位数字之和为288，求x的值.

解析：

　　因为1，4，5，x四个数字不同，排成的四位数中1在千位数字上、百位数字上、十位数字上、个位数字上分别有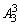个，所以，所有的1的和共为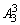4×=24.

　　同理，排成的四位数中4在千位数字上、百位数字上、十位数字上、个位数字上分别有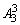个，所有的4的和共为4×4×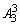=96.

　　所有的5的和共为5×4×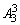=120.

　　所有的x的和共为x×4×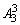=24x.

　　即24x＋120＋96＋24=288，

　　解得：x=2.

例4、将一个四棱锥的每一个顶点染上一种颜色，并使同一条棱上的两个端点颜色不同，如果只有5种颜色可以使用，求不同的染色方案．

解析：

　　设四棱锥为S—ABCD，设先对S染色，有5种不同染色方法；再对A染色有4种不同染色方法；若A、C同色，则对B、D染色分别有3种不同方法；否则对C、B、D染色共有3！种不同染色方法；共5×4×12=240种不同染色色方法．

例5、已知i，m，n是正整数，且1<i≤ m<n，证明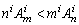

解析：

　　考虑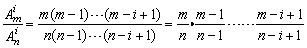

　　因为1< i≤ m < n，所以.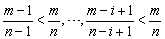

　　所以，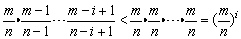

　　即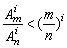：成立.

　　所以原命题成立．

-END-