一、选择题

1、设集合A={a，b，c，d}，B={1，2，3}，f是从A到B的映射，则这样的f共有（　）

A．81个　　　　　　　　　　　　　　　B．64个

C．24个　　　　　　　　　　　　　　　D．12个

2、从0，1，2，…9这10个数字中，任取两个不同数字作为平面直角坐标系中点的坐标，能够确定不在x轴上的点的个数是（　）

A．100　　　　　　　　　　　　　　　 B．90

C．81　　　　　　　　　　　　　　　　D．72

3、已知集合M={1，-2，3}，N={－4，5，6，－7}，从两个集合中各取一个元素作点的坐标，则在直角坐标系中，第一，第二象限不同点的个数有（　）

A．18　　　　　　　　　　　　　　　　B．16

C．14　　　　　　　　　　　　　　　　D．10

4、设a∈N＋，且a<27，则(27－a)(28－a)…(34－a)等于（　）

A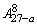．　　　　　　　　　　　　　　 B．

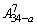C．　　　　　　　　　　　　　　 D．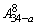

5、某班一天上午要上语文、数学、外语和体育四节课，且要求体育不排在第一、四节、语文不排在第一、二节，则不同的排课方案有（　）

A．2种　　　　　　　　　　　　　　　 B．4种

C．6种　　　　　　　　　　　　　　　 D．8种

6、在一次联欢晚会上，原定的5个节目已排定顺序，在晚会开演前又准备新增2个节目，若这两个新增节目可以随意排入原节目单中，则共有不同的排入方法有（　）

A．48种　　　　　　　　　　　　　　　B．42种

C．30种　　　　　　　　　　　　　　　D．20种

7、在由数字1,2,3,4,5组成的所有没有重复数字的5位数中，大于23145且小于43521的数共有（　）

A.56个　　　　　　　　　　　　　　　 B.57个

C.58个　　　　　　　　　　　　　　　 D.60个

8、从数字1，2，3，5，7中任取2个作为对数的底数和真数，一共可以得到不同的对数值的个数是（　）

A．13　　　　　　　　　　　　　　　　B．12

C．20　　　　　　　　　　　　　　　　D．60

9、如图，用5种不同的颜色给图中A，B，C，D四个区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不同，则共有不同的涂色方法种数为（　）

A．120　　　　　　　　　　　　　　　 B．180

C．240　　　　　　　　　　　　　　　 D．300

10、设集合A={－1，0，1}，B={2，3，4，5，6}，从A到B的映射f满足条件：对每个x∈A，有f(x)﹢x为偶数，那么这样的映射f的个数是（　）

A．6　　　　　　　　　　　　　　　　 B．7

C．12　　　　　　　　　　　　　　　　D．15