|
第I卷(选择题共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、若-1<b<0<a,则下列不等式成立的是( )
A.a>ab2>ab B.ab>ab2>a
C.ab2>a>ab D.ab2>ab>a
2、倾斜角是钝角的直线3x-ay-a=0在两条坐标轴上的截距之差的绝对值是|a|,则实数a=( )
A.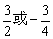 B. B.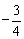
C.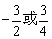 D. D.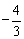
3、若双曲线 的离心率e∈(1,2),则k的取值范围是( ) 的离心率e∈(1,2),则k的取值范围是( )
A.(-∞,1) B.(-3,0)
C.(-12,0) D.(-60,-12)
4、已知抛物线x2-4y=0,则其焦点坐标和准线方程分别为( )
A.F(1,0),x=-1 B.F(0,1),y=-1
C.F(-1,0),x=1 D.F(0,-1),y=1
5、圆x2+y2+2ax+by+1=0的圆心是(1,-2),则该圆的半径r=( )
A.1 B.2
C.3 D.4
6、若a、b∈(0,1),且a≠b,则下列各式中取值最大的是( )
A.a2+b2 B.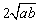
C.2ab D.a+b
7、两个村庄分别位于点(3,1)和点(-4,6)处,已知一条公路3x-2y+a=0从两个村庄间穿过(从安全角度出发,公路不能过任何一个村庄),则实数a的取值范围是( )
A.a<-24,或a>7 B.-24<a<7
C.a<-7,或a>24 D.-7<a<24
8、若方程y2-(lga)x2= -a表示两个焦点都在x轴上的椭圆,则a的取值范围是( ) -a表示两个焦点都在x轴上的椭圆,则a的取值范围是( )
A.a>0 B.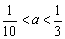
C.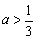 D.以上都不对 D.以上都不对
9、已知双曲线3mx2-my2=3中,给出的下列四个量①渐近线;②焦距;③焦点坐标;④离心率.其中与参数m无关的是( )
A.①② B.②③
C.③④ D.①④
10、点(2,1)是椭圆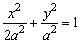 上的点,则该椭圆的长轴长是( ) 上的点,则该椭圆的长轴长是( )
A.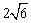 B. B.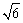
C. D. D.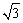
11、方程(4x2+y2-4)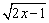 =0的图形是(见下列图形中的实线部分)( ) =0的图形是(见下列图形中的实线部分)( )
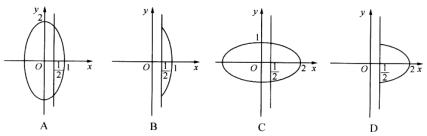
12、已知集合P={x|3-x≥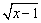 },Q={x|x2-(1+a)x+a≤0},当P },Q={x|x2-(1+a)x+a≤0},当P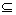 Q时,实数a的取值范围是( ) Q时,实数a的取值范围是( )
A.a≥5 B.a≥3
C.a≥2 D.a≥1
[提示]
二、填空题(本大题共4小题,每小题4分,共16分.把正确答案填在题中横线上.)
13、若点P(4,a)到直线4x-3y=1的距离不大于3,则a的取值范围是_________.
14、设z=2y-2x+4,式中x、y满足条件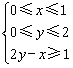 ,则z的最大值是_________. ,则z的最大值是_________.
15、P是圆x2+y2=1上任意一点,过P作两条倾角分别为45°和135°的直线与x轴交于点Q、R,与y轴交于点S、T,则S△PQR+S△PTS=_________.
16、设双曲线C1、C2的方程分别为 ,其离心率分别为e1、e2,给出下列命题: ,其离心率分别为e1、e2,给出下列命题:
①若 ,则C1、C2是共轭双曲线; ,则C1、C2是共轭双曲线;
②若C1与C2有相同的渐近线,则C1与C2是共轭双曲线;
③若C1、C2是共轭双曲线,则e1-2+e2-2=1;
④若C1、C2是共轭双曲线,则它们的四个焦点必为一个正方形的四个顶点;
⑤若e1=e2,则C1与C2必有相同的渐近线.
其中正确命题的序号是_________.
[答案与提示]
三、解答题(本大题共6小题,共74分.解答应写出必要的文字说明、证明过程或演算步骤.)
17、(本小题满分12分)
已知方程kx2+5y2=5k(k∈R),
(1)若方程的图形是一条直线,求k的值;
(2)若方程的图形是一个圆,求该圆的半径;
(3)若方程表示的椭圆过点P( ,-2),求该椭圆的离心率和准线方程. ,-2),求该椭圆的离心率和准线方程.
[答案]
18、(本小题满分12分)
解关于x的不等式x2-(a+a2)x+a3>0(a∈R).
[答案]
19、(本小题满分12分)
某大桥在涨水时有最大跨度的中央桥孔,如图1所示,已知上部呈抛物线形,跨度为20m,拱顶距水面6m,桥墩高出水面4m,现有一货船水下宽度不超过18m,目前吃水线上部分中央船体高5m,宽16m,且该货船在现在状况下还可多装1000t货物,但每装150t货物,船体吃水线就要上升0.04m,若不考虑水下深度,问:该货船在现在状况下能否直接通过或设法通过该桥孔?为什么?
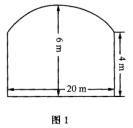
[答案]
20、(本小题满分12分)
图2中实线部分是抛物线y2=4x的一段曲线与椭圆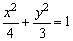 的一段曲线所围成,点N的坐标是(1,0),且A、B两点分别在抛物线的一段和椭圆的一段上,若AB//x轴,求△NAB的周长l的取值范围. 的一段曲线所围成,点N的坐标是(1,0),且A、B两点分别在抛物线的一段和椭圆的一段上,若AB//x轴,求△NAB的周长l的取值范围.

[答案]
21、(本小题满分12分)设a>0,b>0,2c>a+b,求证:
(1)c2>ab;
(2)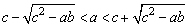 . .
[答案]
22、(本小题满分14分)
已知动点P与双曲线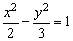 的两个焦点F1、F2的距离之和为定值,且cos∠F1PF2的最小值为 的两个焦点F1、F2的距离之和为定值,且cos∠F1PF2的最小值为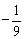 . .
(1)求动点P的轨迹方程;
(2)若有不重合的两点M、N在动点P的轨迹上运动,已知D(0,3)满足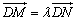 ,求实数λ的取值范围. ,求实数λ的取值范围.
[答案]
|