根号下含有未知量的不等式(如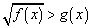 )称无理不等式,解无理不等式的思想是去根号,转化为有理不等式求解.常用去根号的方法是乘方法和换元法. )称无理不等式,解无理不等式的思想是去根号,转化为有理不等式求解.常用去根号的方法是乘方法和换元法.
例1、解不等式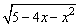 ≥x. ≥x.
分析:解偶次方根的无理不等式的思想也是将其等价转化为有理不等式,转化时先要考虑不等式的两边非负,然后才能运用不等式两边乘方的性质,其次再考虑一边为负的情形.
解答:原不等式等价下列不等式组:
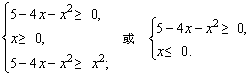
解之,得 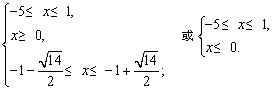
故原不等式的解集为 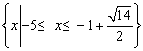 . .
点评:本题也可利用数形结合的思想借助于方程的曲线或函数的图象来解决.
例2、(全国联赛试题)已知:当x∈[0,1]时,不等式 x2cosθ-x(1-x)+(1-x)2sinθ>0恒成立,试求θ的取值范围.
分析:由于二次不等式与二次函数之间有着密切的关系,因此,可将这个含参的二次不等式问题转化为二次函数来研究.
解析:将所给的不等式变形为
(1+sinθ+cosθ)x2-(1+2sinθ)x+sinθ>0.
令f(x)=(1+sinθ+cosθ)x2-(1+2sinθ)x+sinθ
则f(x)>0在闭区间上恒成立,由此可知,必有f(0)>0,f(1)>0,
即f(0)=sinθ>0,f(1)=cosθ>0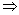 θ在第一象限内. θ在第一象限内.
不妨暂取θ∈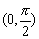 . .
由sinθ>0,cosθ>0可知:1+sinθ+cosθ>0,
二次函数f(x)的图象开口向上.
对称轴方程为 x=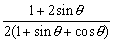 , ,
显然 0<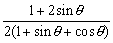 <1, <1,
即对称轴位于闭区间[0,1]内,如图所示.
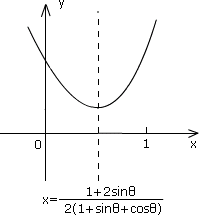
要使f(x)>0在闭区间[0,1]上恒成立,只须满足条件△<0即可.
由△=(1+2sinθ)2-4sinθ(1+sinθ+cosθ)<0.
得sin2θ>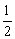 ,由于θ∈ ,由于θ∈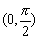 ,2θ∈(0,π). ,2θ∈(0,π).
∴ 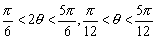 . .
由此可得符合条件的角θ的范围是:
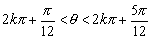 (k∈Z) (k∈Z)
小结:将二次不等式问题转化为二次函数来研究,是一种重要而常用的数学方法,通过这种转化,可以将数和形结合起来,使所给问题,尤其是二次不等式的含参问题得到直观而简捷的解决.
-END- |