从近年全国高考试题来看,有关绝对值不等式的试题每年一般是以一道选择题或填空题来考查一些基本不等式问题,有时与简易逻辑知识里的充要条件联系起来,另外有时以解答题出现考查不等式的证明,以及与二次函数知识联系起来,综合考查学生的函数思想,数形结合思想,分类讨论思想.考查不等式知识常与数学建模联系起来,考查数列、三角函数等知识,并把它应用于解决实际问题.
例1、(辽宁)设全集U=R.
(1)解关于x的不等式|x-1|+a-1>0(a∈R);
(2)记A为(1)中不等式的解集,集合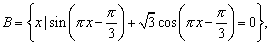
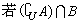 恰有3个元素,求a的取值范围. 恰有3个元素,求a的取值范围.
分析: 本题是一个综合运用绝对值不等式、集合、三角函数知识的题目,依据条件结合定义求解.
解答: (1)由|x-1|+a-1>0得| x-1|>1-a. 当a>1时,解集是R;
当a≤1时,解集是{x|x<a或x>2-a}.
(2)当a>1时,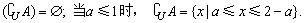
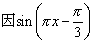 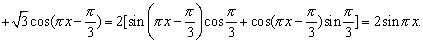
由sinπx=0,得πx=kπ(k∈Z),即x=k∈Z,所以B=Z.
若(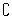 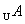 )∩B恰有3个元素, )∩B恰有3个元素,
a>1,  = =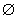 ,( ,(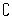 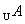 )∩B= )∩B=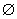 ∩B= ∩B= 要求不能成立 要求不能成立
a≤1,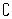 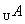 ={x|a≤x≤2-a},B=Z ={x|a≤x≤2-a},B=Z
那么,a=1肯定不行.
恰有的3个元素应是0,1,2.所以
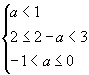 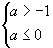 ∴ -1<a≤0 ∴ -1<a≤0
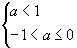 ∴ -1<a≤0 ∴ -1<a≤0
所求的a的取值范围为-1<a≤0
点评: 此题要注意分类讨论.(1)中|x|>a时有a>0和a≤0两种情况,(2)中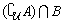 恰有3个元素时a满足的条件. 恰有3个元素时a满足的条件.
例2、(全国理)已知C>0,设P:函数y=Cx在R上单调递增,Q:不等式x+|x-2c|>1的解集为R.如果P和Q有且仅有一个正确,求C的取值范围.
分析:本题主要考查集合、函数、不等式、绝对值等基础知识,考查分析和判断能力,关键是x+|x-2c|>1的解集为R,如何求C.
解析:函数y=cx在R上单调递增 0<c<1. 0<c<1.
不等式 x+|x-2c|>1 |x-2c|>1-x. |x-2c|>1-x.
 x-2c>1-x或x-2c<x-1 x-2c>1-x或x-2c<x-1
 2x>2c+1 或 -2c<-1. 2x>2c+1 或 -2c<-1.
显然,当且仅当-2c<-1成立,x+|x-2c|>1的解为R,故c> . .
∴ 当P正确,且Q不正确,则0<c≤ , ,
当P不正确,且Q正确,则c≥1.
所以C的取值范围是(0,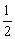 ]∪[1,+∞). ]∪[1,+∞).
例3、(天津理)
解关于x的不等式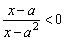 (a∈R) (a∈R)
分析: 分式不等式应化为整式不等式来求解进行分域讨论.
解答: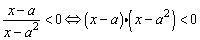
(1)若a=0,则a=a2=0,故不等式为:x2<0,解集为Φ;
(2)a=1,则a=a2=1,故不等式为(x-1)2<0,无解,解集为Φ;
(3)若0<a<1,则a2<a,所以a2<x<a,故解集为{x|a2<x<a};
(4)若a<0或a>1,则a2>a,∴a<x<a2.
故解集为{x|a<x<a2}.
[点评] 解各种不等式的基本思路是应用合适的运算把原不等式化为整式不等式,再经因式分解,用零点划分取区间的办法求解,还应注意对不等式中所含参数进行讨论.
例4、(全国高考试题)已知实数a、b、c是实数,函数f(x)=ax2+bx+c,g(x)=ax+b,当-1≤x≤1时,|f(x)|≤1.
(Ⅰ)证明:|c|≤1;
(Ⅱ)证明:当-1≤x≤1时,|g(x)|≤2;
(Ⅲ)设a>0,当-1≤x≤1时,g(x)的最大值为2,求f(x).
分析:本题主要考察二次函数的性质,含有绝对值不等式的性质,以及综合运用数学知识分析问题和解决问题能力,因此要从二次函数的性质出发.
解答:(Ⅰ)∵ 当-1≤x≤1时,f(x)≤1,
∴ 取x=0,得 |c|=|f(0)|≤1,
即 |c|≤1.
(Ⅱ)1°当a>0时,g(x)=ax+b在[-1,1]上是增函数,
∴ g(-1)≤g(x)≤g(1).
∵ |f(x)|≤1(-1≤x≤1),|c|≤1,
∴ g(1)=-a+b=-f(-1)+c≥-(|f(-1)|+|c|)≥-2,
由此得 |g(x)|≤2.
2°当a<0时,g(x)=ax+b在[-1,1]上是减函数,
∴ g(-1)≥g(x)≥g(1).
∵ |f(x)|≤1(-1≤x≤1),|c|≤1
∴ g(-1)=-a+b=-f(-1)+c≤|f(-1)|+|c|≤2,
g(1)=a+b=f(1)-c≥(|f(1)|+|c|)≥-2,
由此得 |g(x)|≤2
3°当a=0时,g(x)=b,f(x)=bx+c.
∵ -1≤x≤1
∴ |g(x)|=|f(1)-c|≤|f(1)|+|c|≤2.
综上,得 |g(x)|≤2.
(Ⅲ)∵ a>0,g(x)在[-1,1]上是增函数,当x=1时取得最大值2,
即g(1)=a+b=f(1)-f(0)=2,①
∵ -1≤f(0)=f(1)-2≤1-2=-1,
∴ c=f(0)=-1,
∵ 当-1≤x≤1时,f(x)≥-1,即 f(x) ≥f(0).
根据二次函数性质,直线x=0为f(x)的图象的对称轴,由此得
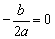 , 即 b=0. , 即 b=0.
由①得a=2, ∴ f(x)=2x2-1.
|