多面体是立体几何中考查同学们各种数形间的转换的载体.尽管各种几何体千差万别,但仍具有某些“共性”,这些“共性”是解题的关键.如平行于底面的柱、锥体的截面是与底面相似的图形,这使我们得以应用相似形知识解题.在棱锥里常常应用一系列直角三角形解题,这些都是将空间立体几何问题转化成平面几何问题.特别是新教材中新增加了研究性课题:简单多面体的欧拉定理,意味着我们研究多面体知识将要上升到一个理论高度,不再仅仅局限于几种常见的多面体,而应发展到一般的多面体,通过欧拉定理来研究它们的顶点数,面数,棱数间的关系,并学会利用它解决一些较抽象、较复杂的分子结构问题,从而将数学基础科学与化学等自然科学联系起来,这是顺应我国培养知识全面、综合能力强的教育目标.
例1、(全国卷I)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且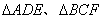 均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )
均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )
A.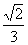 B.
B.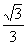
C.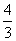 D.
D.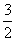
分析:将多面体分割成简单的多面体的体积求解。
解:
如图,过A、B两点分别作AM、BN垂直于EF,垂足分别为M、N,连结DM、CN,可证得DM⊥EF、CN⊥EF,多面体ABCDEF分为三部分,多面体的体积V为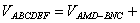
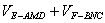 ,
,
∵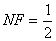 ,
,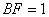 ,∴
,∴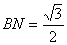 ,
,
作NH垂直于点H,则H为BC的中点,
则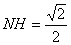 ,∴
,∴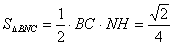 ,
,
∴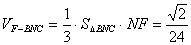 ,
,
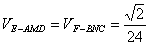 ,
,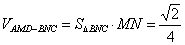 ,
,
∴ ,故选A.
,故选A.
例2、(全国Ⅱ)将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为
A.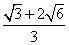 B.2+
B.2+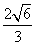
C.4+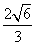 D.
D.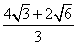
解析:
显然4个钢球两两相切且每个钢球与四面体也相切时,这个正四面体的高最小。这时4个钢球的球心构成一个小正四面体,其底面中心到大正四面体距离是小钢球的半径1,设小正四面体顶点距大正四面体顶点为x,大正四面体的棱长为a,高为h,小正四面体的高为m,则h=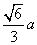 ,m=
,m=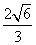 ,大正四面体底面中心到底面边的距离n=
,大正四面体底面中心到底面边的距离n=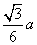 ,侧面斜高y=
,侧面斜高y=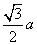 ,由平几知识可得
,由平几知识可得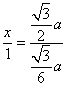 =3,得x=3,故h=3+1+m=4+
=3,得x=3,故h=3+1+m=4+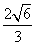 ,选C.
,选C.
答案:C