最值与定值
最值问题包括长度的最值,可展曲面的最短线路、角度的最值以及面积的最值等问题.在复习最值等问题时,应根据题目条件,把多余问题“单一化”,写出相应的目标函数,再用代数中的一些求值的方法求出最值来.在立体几何中,证明定值问题通常有两种方法:一是直接法,即从已知条件出发(一般情况),直接进行推理、计算,并求出定值;二是特殊值法,即先由特殊情况(或极限情况),估计出定值,然后对一般情况,证明它等于这个定值.
例1、如图,在棱长为a的正方体ABCD—A1B1C1D1中,过BD1的截面分别交AA1、CC1于E、F点,求四边形BED1F面积的最小值.
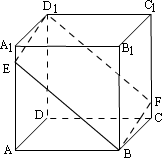
分析:
显然截面BED1F为平行四边形,且此平行四边形的对角线BD1为定值 ,故欲求四边形面积的最小值即求E到BD1的距离最小值. ,故欲求四边形面积的最小值即求E到BD1的距离最小值.
解析:
由以上分析知,欲求E到BD1的最小距离,即求异面直线AA1和BD1间的距离,另求得这个距离为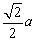 .从而平行四边形BED1F面积最小值为 .从而平行四边形BED1F面积最小值为
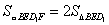 =2× =2×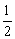 × ×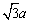 · · = =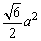 . .
例2、正四棱柱ABCD—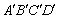 中,P为对角线 中,P为对角线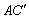 上一动点,设PC与面AC所成的角为 上一动点,设PC与面AC所成的角为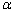 ,PD与面 ,PD与面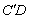 所成的角为 所成的角为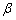 .求证:tan .求证:tan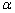 ·tan ·tan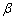 为定值. 为定值.
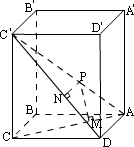
分析:
如图所示,欲证tan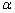 ·tan ·tan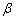 为定值,首先应把tan 为定值,首先应把tan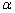 ·tan ·tan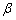 用正四棱柱的某些元素表示出来,方可证出. 用正四棱柱的某些元素表示出来,方可证出.
解析:
∵P在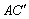 上运动,∴可设PA=x. 上运动,∴可设PA=x.
作PM⊥AC,在Rt△PCM中,tan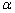 = = ① ①
又∵PM∥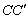 ,∴ ,∴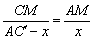 ② ②
即CM=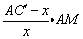 ,②代入①得 ,②代入①得
tan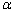 = =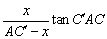 ,同理,过点P作PN⊥ ,同理,过点P作PN⊥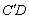 ,可得 ,可得
tan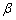 = =
∴ tan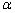 ·tan ·tan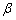 = =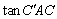 · ·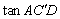 (定值). (定值).
|