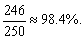线性规划是新教材新增的内容之一，它是数学规划中理论较完整、方法较成熟、应用广泛的一个分支，它可以解决科学研究、工程设计、经济管理等许多方面的实际问题，鉴于其在生产生活实践中经常用到，很有可能成为高考中应用题的一个新类型，应予以重视.

例1、（北京·春季高考）在直角坐标系xOy中，已知△AOB三边所在直线的方程分别为x=0，y=0，2x＋3y=30，则△AOB内部和边上整点（即横、纵坐标均为整数的点）的总数是（）

A、95　　　　　　B、91　　　　　　　　C、88　　　　　　　D、75

解析：由2x＋3y=30，得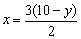，为得到整点，即找出y∈[0,10]内的整数.

所以AB边上的整点有（2，8），（6，6），（9，4），（12，2），及B（15，0），A（0，10）共6个点.

如图长方形OB，OA边上各有16和11个整点.所以长方形内部和边上的整点共16×11个.

因而AB边上有6个整点，由对称性设△AOB和△ABC有整点x个，不包括AB边上的整点.

则2x＋6=16×11，即x=8×11－3=85.

所以△ABC内部和边上的整点是85＋6=91.

故应选B.

评注：本题主要考查直角坐标系、直线方程以及三角形的整点等基本知识和运算能力，题目虽小，但对思维能力要求较高.

另解：可用网格法，如下图．

　可知有91个整点，故选B.

答案：B

例2、（全国高考试题）某电脑用户计划使用不超过500元的资金购买分别为60元、70元的单片软件和盒装软件，根据需要，软件至少买3片，磁盘至少买2盒，则不同的选购方式共有（　）

A、5种　　　　　B、6种　　　　　　　C、7种　　　　　　　　D、8种

分析：本题实际考查的是线性规划，可先列出线性约束条件，再去求其整点解的个数.

解答：设买x张软件，y盒磁盘，则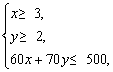

　即

　分别取符合题意的x,y如下：

（1）x=3时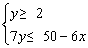，∵ 即：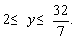

　　此时，y=2，3，4．

（2）x=4时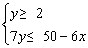，∵ 即：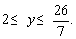

　　 ∴ 取y=2,3．

（3）x=5时，此时 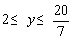，∴y=2.

（4）x=6时，y=2，而x>6时，y<2不合题意.

可知，有7种不同的选购方式，为：

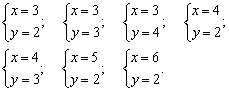
故选C.

例3、（高考模拟试题）某工厂有一批长2.5米的条形钢材，要截成60厘米和42厘米的两种规格的零件毛坯，找出最佳的下料方案，并计算材料的利用率.

分析：本题可转化为线性规划问题求解，考查分析问题和解决问题能力.

解答：设截成60cm的x根，42cm的y根，

　则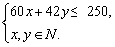

　即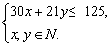

　使30x＋21y较大且符合不等式的x,y有

　

　计算得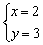 时，60x＋42y最大为 60×2＋42×3=246.

　此时，材料利用率最高，下料方案最佳.

　此时利用率为

-END-