1、已知实数x、y满足2x＋y≥1，求u=x2＋y2＋4x－2y的最小值.

解析：注意到所求式的结构特点，学生容易想到将其作如下的配方变形.

　u=(x＋2)2＋(y－1)2－5.

　显然，(x＋2)2＋(y－1)2表示点P（x、y）与定点A（－2，1）的距离的平方.

　由约束条件2x＋y≥1知，点P（x、y）在直线l：2x＋y=1的右上方区域G.

　于是，问题转化为求定点A（－2，1）到区域G的最近距离.

　由图知，点A到直线l的距离为A到区域G中点的距离的最小值.

　

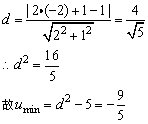
2、设实数x、y满足不等式组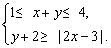

（1）求点（x，y）所在的平面区域；

（2）设a>－1，在（1）所求的区域内，求函数f(x，y)=y－ax的最值.

解析：必须明确，求点（x，y）所在的平面区域，关键是确定区域的边界线，可从去掉绝对值符号入手.

（1）已知的不等式组等价于

解得点（x，y）所在的平面区域为所示的阴影部分（含边界）.其中，

AB：y=2x－5；BC：x＋y=4；

CD：y=－2x＋1；DA：x＋y=1.

（2）f（x，y）表示直线l：y－ax=k在y轴上的截距，且直线l与（1）中所求区域有公共点.

∵ a>－1，

∴ 当直线l过顶点C时，f（x、y）最大.

∵ C点的坐标为（－3，7），

∴ f(x、y)的最大值为7＋3a.

如果－1<a≤2，那么当直线l过顶点A（2，－1）时，f（x，y）最小，最小值为－1－2a.

如果a>2，那么当直线l过顶点B（3，1）时，f（x，y）最小，最小值为1－3a.

-END-