求异面直线距离在过去的高考中一直未作重点要求,但在求解过程中许多数学思想可得以应用,作为课外思考与练习,可提高我们分析、解决问题的能力.
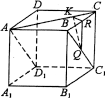
例:正方体ABCD-A1B1C1D1棱长为a,求异面直线AC与BC1的距离.
分析:
求异面直线的距离可以根据定义直接作出异面直线的公垂线段并求出其长度,也可以转化为直线与其平行平面间的距离来求,还可以利用函数求极值或通过向量,空间直角坐标等求解.
解析:
方法1:如图,连BA1,BC1,A1C1,则AC∥平面BA1C1.
设O,M分别是AC,BB1的中点,连AM,CM,OM,B1D.
则OM∥B1D.又B1D⊥面BA1C1,∴OM⊥面BA1C1.

∴面AMC⊥面BA1C1,且面AMC∩BA1C1=PQ,则AC∥PQ.
作QH⊥PQ,则QH⊥面BA1C1,且QH为AC,BC1的公垂线段.
∵BM∥CC1,∴△BMQ∽△C1CQ.
又△BM= C1C,∴MQ= C1C,∴MQ=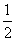 CQ,∴CQ= CQ,∴CQ=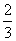 CM. CM.
有△MAC中,MA=MC= ,AC= ,AC=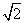 a,MO⊥AC. a,MO⊥AC.
∴MQ=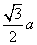 ,∴QH= ,∴QH=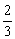 MO= MO= . .
方法2:如图,取BC的中点P,连结PD,PB1分别交于AC,BC1于M,N两点.
易证DB1∥MN,DB1⊥AC,DB1⊥BC1.
∴MN为异面直线AC与BC1的公垂线段,易求MN=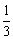 B1D= B1D=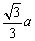 . .
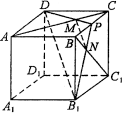
方法3:如图,∵AC∥平面A1C1B,
∴AC与BC1的距离等于AC与平面A1C1B的距离.

设上、下底面的中心分别为O,O1,连O1B.
∵A1C1⊥O1B1,由三垂线定理知,A1C1⊥O1B.
∴A1C1⊥面O1OB,∴面O1OB⊥面A1C1B.
作OE⊥O1B于E,则OE⊥面A1C1B,则OE的长为AC与平面A1C1B的距离.
∵OB=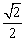 a,OO1=a,∴O1B= a,OO1=a,∴O1B= a, a,
∴OE= . .
方法4:如图,∵平面ACD1∥平面A1C1B,
∴AC与BC1的距离等于平面ACD1与平面A1C1B的距离.
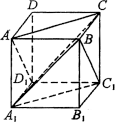
由本课时例1知,平面ACD1与平面A1C1B的距离为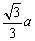 . .
方法5:如图,任取点Q∈BC1,作QR⊥BC于R点,作RK⊥AC于K点,
设RC=x,则BR=QR=a-x,CK=KR,
∴KR2=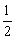 CR2= CR2= x2. x2.
则QK2=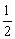 x2+(a-x)2= x2+(a-x)2=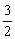 (x- (x- a)2+ a)2+ a2≥ a2≥ a2 a2
故QK的最小值,即AC与BC1的距离等于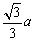 . .
方法6:如图,以C为原点建立空间直角坐标系,
则C(0,0,0),B(a,0,0),A(a,a,0),C1(0,0,a).
在BC1上取一点P,设BP=x,作PQ⊥BC于Q,则PQ⊥平面ABCD.

作QR⊥AC于R,由三垂线定理,知PR⊥AC,
有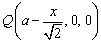 , ,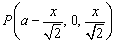 ,而△CRQ为等腰直角三角形, ,而△CRQ为等腰直角三角形,
∴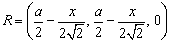 . .
 . .
由于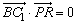 ,即 ,即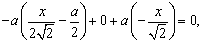
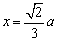 . 代入 . 代入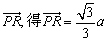 ,即为所求. ,即为所求.
|