|
一、选择题(本题共12小题,每小题5分,共60分,在每小题后给出的四个选项中,只有一项是符合题目要求的.)
1、对于已知直线a,如果直线b同时满足三个条件:
(1)与a成异面直线;
(2)与a所成的角为定值θ;
(3)与a的距离为定值d.
那么,这样的直线b有( )
A.1条 B.2条
C.3条 D.无穷多条
2、已知长方体ABCD—A1B1C1D1中,棱A1A=5,AB=12,那么直线B1C1和平面A1BCD1的距离是( )
A.5 B.
C.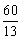 D.8 D.8
3、在直角坐标系中,设A(-2,3),B(3,-2).沿x轴把直角坐标平面折成120°的二面角后,AB的长为( )

4、一条直线与直二面角的两个面所成的角分别为α和β,则α+β的取值范围是( )

5、直线a是平面α的斜线,b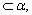 当a与b成60°的角,且b与a在α内的射影成45°时,a与α所成的角是( ) 当a与b成60°的角,且b与a在α内的射影成45°时,a与α所成的角是( )
A.60° B.45°
C.90° D.135°
6、已知平面α内有∠XOY=60°,OA是α的斜线,且OA=10,∠AOX=∠AOY=45°,则A到α的距离是( )

7、夹在两个平面间的两条线段之和为342cm,它们在其中一个平面内的射影长分别是78cm及36cm,则这两个平行平面之间的距离是( )
A.82cm B.164cm
C.80cm D.160cm
8、相交成90°的两条直线和一个平面所成的角分别是30°和45°,则这两条直线在该平面上的射影所成的锐角是( )
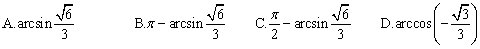
9、已知正方形ABCD,沿对角线AC将三角形ADC折起,设AD与平面ABC所成角为β,当β取最大值时,二面角B-AC-D等于( )
A.45° B.90°
C. D. D.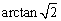
10、在二面角M-l-N的面M内有-Rt△ABC,斜边BC在棱l上,若A在平面N内的射影为D,∠ACD=θ1,∠ABD=θ2,二面角为θ,则有( )
A.cos2θ=cos2θ1+cos2θ2
B.sin2θ=sin2θ1+sin2θ2
C.tan2θ=tan2θ1+tan2θ2
D.sin2θ=cos2θ1+cos2θ2
11、在60°的二面角α-a-β的面α内,AB⊥a于B,AB=2,在面β内,CD⊥a于D,CD=3,BD=1,M是a上的一个动点,则AM+CM的最小值为( )

12、如图,在水平横梁上A,B两点处各挂长为50cm的细线AM、BN,AB的长度为60cm,在MN处挂长为60cm的木条,MN平行于横梁,木条中点为O,若木条绕O的铅垂线旋转60°角,则木条比原来升高了多少( )
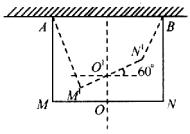
A.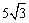 B.5cm B.5cm
C.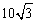 D.10cm D.10cm
二、填空题(本大题共4个小题,每小题4分,共16分,把正确答案填在题中横线上.)
13、在60°的二面角α-l-β中,动点A∈α,动点B∈β,AA1⊥β,垂足为A1,且AA1=a,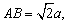 那么点B到平面α的最大距离是_________. 那么点B到平面α的最大距离是_________.
14、矩形ABCD中,AB>BC,点P为对角线上一点,且 MP⊥面AC,若二面角M-AB-C,M-BC-A,M-CD-A,M-AD-B分别是θ1,θ2,θ3,θ4,那么其中_______最大,________最小. MP⊥面AC,若二面角M-AB-C,M-BC-A,M-CD-A,M-AD-B分别是θ1,θ2,θ3,θ4,那么其中_______最大,________最小.
15、正方形ABCD的边长为2,E,F分别是AB和CD的中点,将正方形沿EF折成直二面角,如图M为矩形AEFD内一点,如果∠MBE=∠MBC,MB和平面BCF所成角的正切值为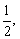 那么点M到直线EF的距离为________________. 那么点M到直线EF的距离为________________.
16、α,β是两个不同的平面,m,n是平面α及β之外的两条不同直线,给出四个判断:
①m⊥n ②α⊥β ③n⊥β ④m⊥α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:_____.
[答案] 三、解答题(本大题共6小题,前5小题每小题12分,最后1小题14分,共74分,解答应写出必要的文字说明,证明过程或演算步骤.)
17、长方体ABCD-A1B1C1D1中,AB=BC=a,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°.试求:
(1)截面EAC的面积;
(2)异面直线A1B1与AC之间的距离.
[答案]
18、在正方体ABCD-A1B1C1D1中,棱长为a.
(1)求证:平面AB1D1∥平面C1BD;
(2)求平面AB1D1和平面C1BD间的距离.
[答案]
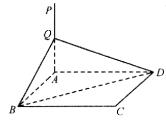
19、如图,已知ABCD是矩形,AB=3,AD=4,PA⊥平面ABCD,PA=4,Q是PA的中点.求:
(1)点Q到BD的距离;
(2)点P到平面BQD的距离.
[答案]
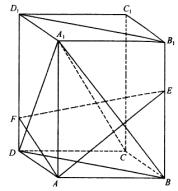
20、如图,在长方体ABCD-A1B1C1D1中,点E、F分别在BB1、DD1上,且AE⊥A1B,AF⊥A1D.
(1)求证:A1C⊥平面AEF;
(2)若规定两个平面所成的角是这两个平面所组成的二面角中的锐角(或直角),则在空间中有定理:若两条直线分别垂直于两个平面,则这两条直线所成的角与这两个平面所成的角相等.
试根据上述定理,在AB=4,AD=3,AA1=5时,求平面AEF与平面D1B1BD所成角的大小.(用反三角函数值表示)
[答案]
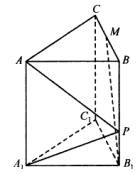
21、如图,正三棱柱ABC-A1B1C1的各棱长都是2,M是BC的中点,P是侧棱BB1上一点,且A1P⊥B1M.
(1)试求A1P与平面APC所成角的大小;
(2)求点A1到平面APC的距离.
[答案]
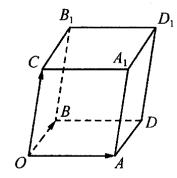
22、如图,已知向量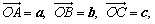 可构成空间向量的一组基底,若a=(a1, a2, a3), b=(b1,b2, b3), c=(c1, c2, c3),在向量已有的运算法则基础上,新定义一种运算a×b=(a2b3-a3b2, a3b1-a1b3, a1b2-a2b1).显然a×b的结果仍为一向量,记作p. 可构成空间向量的一组基底,若a=(a1, a2, a3), b=(b1,b2, b3), c=(c1, c2, c3),在向量已有的运算法则基础上,新定义一种运算a×b=(a2b3-a3b2, a3b1-a1b3, a1b2-a2b1).显然a×b的结果仍为一向量,记作p.
(1)求证:向量p为平面OAB的法向量;
(2)求证:以OA,OB为边的平行四边形OADB面积等于|a×b|;
(3)将得到四边形OADB按向量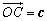 平移,得到一个平行六面体OADB-CA1D1B1,试判断平行六面体的体积V与|(a×b)·c|的大小. 平移,得到一个平行六面体OADB-CA1D1B1,试判断平行六面体的体积V与|(a×b)·c|的大小.
[答案]
|