|
一、选择题(本大题共12小题,每小题5分,共60分,每小题只有唯一正确答案)
1、在下列条件中,能够判定平面M与平面N平行的是( )
A.M、N都垂直于平面θ
B.M内不共线的三点到N的距离相等
C.直线l、m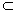 M且l∥N,m∥N M且l∥N,m∥N
D.l、m是两异面直线且l∥M, l∥N,m∥M,m∥N
2、设a、b是两条异面直线,在下列命题中正确的是( )
A.有且仅有一条直线与a、b都垂直
B.有一个平面与a、b都垂直
C.过直线a有且仅有一个平面与b平行
D.过空间中任一点必可作一条直线与a、b都相交
3、下列命题中正确的个数是( )
①四边相等的四边形是菱形;
②若四边形有两个对角都是直角,则这四边形是圆内接四边形;
③“平面不经过直线”的等价说法是“直线上至多有一个点在平面内”;
④若两平面有一条公共直线,则这两平面的所有公共点都在这条公共直线上.
A.1个 B.2个
C.3个 D.4个
4、如图所示,∠BAD=90°的等腰直角三角形ABD与正三角CBD所在平面互相垂直,E是BC的中点,则AE与平面BCD所成角的大小为( )

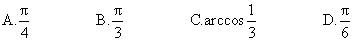
5、已知三条直线m,n,l,三个平面α,β,γ,下面四个命题中正确的是( )

6、如图所示是正方体的平面展开图,在这个正方体中①BM与ED平行;②CN与BE是异面直线;③CN与BM成60°角;④DM与BN垂直.以上四个命题中,正确命题的序号是( )

A.①②③ B.②④
C.③④ D.②③④
7、下列命题中正确的是( )
A.直线a,b异面,过空间内任一点O作OA∥a, OB∥b,则∠AOB叫做异面直线a,b所成的角
B.若∠CBA=∠BAD,那么BC∥AD
C.和两条异面直线都垂直的直线,叫做这两条异面直线的公垂线
D.两条异面直线所成的角只可能是锐角或直角
8、如图所示,在棱长为2的正方体ABCD—A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE与FD1所成的角的余弦值等于( )

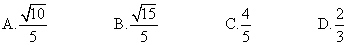
9、在正方体ABCD—A1B1C1D1中,六个面的对角线中与AC成60°角且与AC为异面直线的有( )
A.4条 B.6条
C.8条 D.10条
10、已知直线l、m、n及平面α,下列命题中的假命题是( )
A.若l∥m,m∥n,则l∥n
B.若l⊥α,n∥α,则l⊥n
C.若l⊥m,m∥n,则l⊥n
D.若l∥α,n∥α,则l∥n
11、下列各图是正方体或正四面体,P、Q、R、S分别是所在棱的中点,这四个点不共面的一个图是( )

12、ABCD是空间四边形,AB=CD且AB和CD成30°角,E、F分别是BC和AD的中点,则EF和AB所成的角是( )
A.15° B.30°
C.75° D.15°或75°
[提示]
二、填空题(本大题共4小题,每小题4分)
13、正方体ABCD—A1B1C1D1中,E为DD1的中点,则BD1与过A、C、E的平面的位置关系是______.
14、空间四边形ABCD中,E、F、G、H依次为AB、BC、CD、DA边的中点,且AC=2,BD=4,则EG2+FH2的值是______.
15、在正方体ABCD—A1B1C1D1中,M、N分别是A1D1、C1D1的中点,则直线AA1与梯形AMNC所在平面成的角的正切值为______.
16、已知m、n是直线, α,β,γ是平面,给出下列命题:
①若α⊥β, α∩β=m,n⊥m,则n⊥α或 n⊥β;
②若α∥β, α∩γ=m,β∩γ=n,则m∥n;
③若m不垂直于α,则m不可能垂直于α内的无数条直线;
④若α∩β=m,n∥m且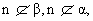 则n∥α且 n∥β 则n∥α且 n∥β
其中正确的命题序号是______.(注:把你认为正确命题的序号都填上)
[答案] 三、解答题(本大题共6小题,共74分,解答应写出必要的文字说明、证明过程或演算步骤)
17、如图所示,在正方体ABCD—A1B1C1D1中,M、N、P分别是C1C、B1C1、C1D1的中点.求证:

(1)AP⊥MN;
(2)平面MNP∥平面A1BD.
[答案]
18、如图所示,P是△ABC所在平面外一点,PA=PB,CB⊥面PAB,M是PC的中点,N是AB上的点,AN=3NB.
(1)求证:MN⊥AB;
(2)当∠APB=90°,BC=2,AB=4时,求MN的长.
[答案]
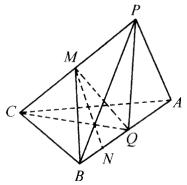
19、已知:空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M、N分别为BC和AD的中点,设AM和CN所成的角为α.求cosα的值.
[答案]
20、如图所示,在Rt△ABC中,∠ACB=90°,PA⊥平面ABC,AE⊥PB,垂足为E,AF⊥PC,垂足为F.
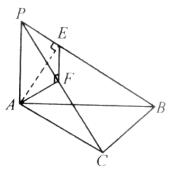
(1)求证:PB ⊥平面AEF;
(2)若PA=AB=2,设∠BPC=θ,试用tanθ表示△AEF的面积,当tanθ为何值时,△AEF的面积最大?并求这个最大值.
[答案]
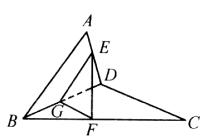
21、如图所示,AB、CD是两条异面直线,AB=CD=3a,E、F分别是线段AD、BC上的点,且ED=2AE,FC=2BF,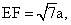 G∈BD,EG∥AB. G∈BD,EG∥AB.
(1)求AB与CD所成的角;
(2)求△EFG的面积.
[答案]
22、如图(1)所示,直线m1:x=-2与x轴、直线n1:y=3、直线n2:y=6分别交于A、D、F三点,直线m2:x=2与x轴、直线n1、直线n2分别交于B、C、E三点,现把四边形ABCD绕x轴逆时针旋转90°,得到四边形ABC1D1,如图(2).
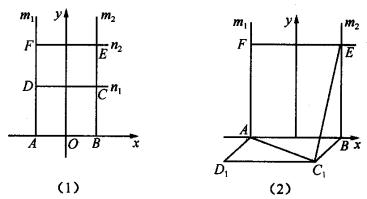
求:(1)直线C1D1与直线EF的距离;
(2)点C1到直线AF的距离;
(3)点D1到平面BEC1的距离;
(4)直线C1E与平面ABEF所成角的大小.
[答案]
|