“向量”知识逐渐成为命题热点，一般选择题，填空题重在考查空间向量的概念，解答题重在考查空间向量的运算及数量积等性质，利用向量知识解决立体几何问题．不过从课本中的例习题的形式来看，高考中对于原立体几何中关于求异面直线所成的角，异面直线间的距离，以及有关证明线线垂直，线面垂直，线线平行，线面平行等问题，一般地都可采用两种方法处理，一种用纯立体几何知识解决，这对思维能力要求较高，另一种就是用向量法解决，这样将几何问题代数化．同学们在平时训练中，对于同一题，最好采取两种方法解决，并且训练熟练．

例1、(全国高考试题)如图，已知：平行六面体ABCD－A1B1C1D1的底面ABCD是菱形,且∠C1CB =∠C1CD =∠BCD = 60°.

　　（1）证明：C1C⊥BD；

　　（2）当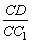的值为多少时，能使A1C⊥平面C1BD？请给出证明．

分析：

　　本题考查直线与直线，直线与平面的关系，逻辑推理能力，怎样把空间垂直关系的判定转化为向量的知识是关键．

解答：

　　

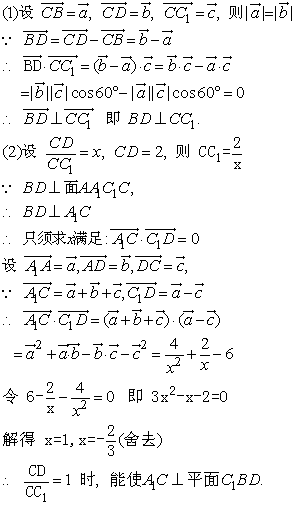
例2、（上海高考试题）若则下列等式不一定成立的是（　）

A．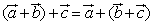

B．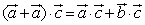

C．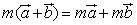

D．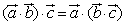

分析：

　　本题考查向量的加、减法及数乘、数量积等运算的性质，空间向量（即使是平面向量）的数量积不满足结合律．故选D．

答案：D

-END-