空间向量在高一学习了平面向量后，在高二下（B）中又重新介绍，可见向量知识的重要性在加强，一方面它既是数学中的重要概念，另一方面它可以计算，并为立体几何中的求角求距离提供了一种很好的工具，因此，在平常的学习中应几何方法和向量方法均会运用，高考中的试题的出现预计一般也应是两种方法均可解出的问题．

例1、（天津高考试题）如图所示，以正四棱锥V—ABCD底面中心O为坐标原点建立空间直角坐标系O—xyz，其中Ox∥BC，Oy∥AB，E是VC中点，正四棱锥底面边长为2a，高为h．

　　（1）求；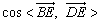

　　（2）记面BCV为α，而DCV为β，若∠BED是二面角α—VC—β的平面角，求∠BED．

分析：

　　本题考查空间直角坐标的概念，空间点和向量的坐标表示以及两个向量的夹角的计算方法；考查运用向量研究空间图形的数学思想方法．

解答：

　　（1）由题意，知B（a,a,0），C(－a,a,0)，D（－a,－a,0）,,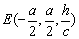

　　　　

　　（2）若∠BED是二面角α—VC—β的平面角，

　　　　

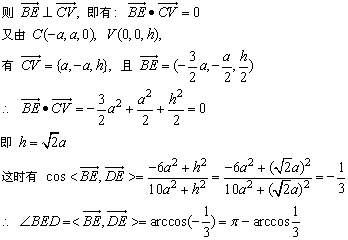
例2、（上海高考试题）如图所示，三棱柱OAB—O1A1B1，平面OBB1O1⊥平面OAB，∠O1OB=60°,∠AOB=90°，且OB=OO1=2，OA=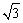，求：

　　（1）二面角O1—AB—O的大小；

　　（2）异面直线A1B与AO1所形成角的大小．

分析：本题主要是应用向量知识求二面角、异面直线所成的角．

解析：

　　（1）取OB的中点D，连结O1D，则O1D⊥OB．

　　　　∵ 平面OBB1O1⊥平面OAB，

　　　　∴ O1D⊥平面OAB．

　　　　过D作AB的垂线，垂足为E，连结O1E，则O1E⊥AB．

　　　　∴ ∠DEO1为二面角O1—AB—O的平面角．

　　　　

　　（2）以O点为原点，分别以OA，OB所在直线为x，y轴，过O点且与平面AOB垂直的直线为z轴，建立空间直角坐标系，则

　　　　

-END-