面面垂直的判定与性质以及二面角,在高考中偶有考查,要熟练掌握所涉及的有关定理以及解决问题的一般方法.
例1、(高考·重庆卷)如图,在四棱锥P—ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC. 已知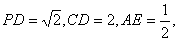 求: 求:
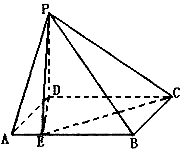
(Ⅰ)异面直线PD与EC的距离;
(Ⅱ)二面角E—PC—D的大小.
分析:根据条件找公垂线和二面角的平面角.
解法一:
(Ⅰ)因PD⊥底面,故PD⊥DE,
又因EC⊥PE,且DE是PE在面ABCD内的射影,
由三垂直线定理的逆定理知EC⊥DE,因此DE是异面直线PD与EC的公垂线.
设DE=x,因△DAE∽△CED,故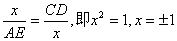 (负根舍去). (负根舍去).
从而DE=1,即异面直线PD与EC的距离为1.
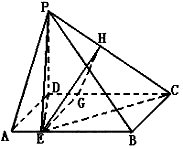
(Ⅱ)过E作EG⊥CD交CD于G,作GH⊥PC交PC于H,连接EH. 因PD⊥底面,
故PD⊥EG,从而EG⊥面PCD.
因GH⊥PC,且GH是EH在面PDC内的射影,由三垂线定理知EH⊥PC.
因此∠EHG为二面角的平面角.
在面PDC中,PD=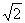 ,CD=2,GC= ,CD=2,GC=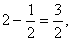
因△PDC∽△GHC,故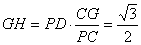 , ,
又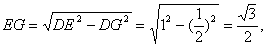
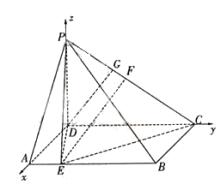
故在 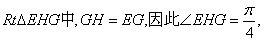
即二面角E—PC—D的大小为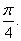
解法二:
(Ⅰ)以D为原点,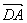 、 、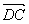 、 、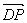 分别为x、y、z轴建立空间直角坐标系. 分别为x、y、z轴建立空间直角坐标系.
由已知可得D(0,0,0),P(0,0,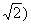 , ,
C(0,2,0)设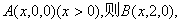
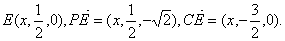 由 由 , ,
即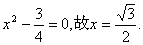 由 由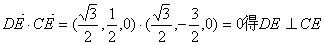 , ,
又PD⊥DE,故DE是异面直线PD与CE的公垂线,易得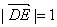 , ,
故异面直线PD、CE的距离为1.
(Ⅱ)作DG⊥PC,可设G(0,y,z).由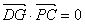 得 得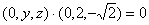
即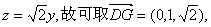 作EF⊥PC于F,设F(0,m,n), 作EF⊥PC于F,设F(0,m,n),
则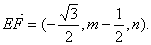
由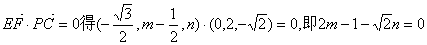 , ,
又由F在PC上得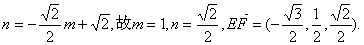
因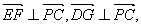 故平面E—PC—D的平面角 故平面E—PC—D的平面角 的大小为向量 的大小为向量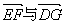 的夹角. 的夹角.
故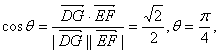 即二面角E—PC—D的大小为 即二面角E—PC—D的大小为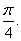
例2、(全国)如果直线 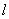 、m与α、β、γ平面满足: 、m与α、β、γ平面满足: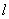 =β∩γ, =β∩γ,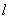 ∥α,m ∥α,m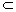 α和m⊥γ,那么必有( ) α和m⊥γ,那么必有( )
A、α⊥γ且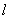 ⊥m B、α⊥γ且m∥β ⊥m B、α⊥γ且m∥β
C、m∥β且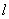 ⊥m D、α∥β且α⊥γ ⊥m D、α∥β且α⊥γ
解答:
依题意,m⊥γ,且m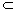 α,则必有α⊥γ, α,则必有α⊥γ,
又因为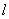 =β∩γ,则有 =β∩γ,则有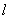 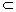 γ, γ,
而m⊥γ,则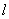 ⊥m. ⊥m.
故选A.
答案:A
例3、(全国)α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个结论:
①m⊥n ②α⊥β ③n⊥β ④m⊥α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题.
解答:
课本上有习题结论:自二面角内一点分别向两个平面引垂线,它们所成角与二面角的平面角互补.
由此结论知应为①③④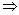 ②或②③④ ②或②③④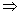 ①. ①.
|