折叠与展开

　　在求二面角的平面角时，常会遇到作平面角较为困难的情况，这里介绍用射影面积法求二面角的平面角的大小.

　　如图，已知△ABC的边BC在平面α内，顶点A不在α内，设△ABC的面积为S，它在平面α内的射影△OBC的面积为S′，且平面α与△ABC所在平面所成的二面角大小为θ（）.

　　求证：.

证明：

　　过A作AD⊥BC于D，连OD.

　　则 OD⊥BC，∠ADO为二面角的平面角.

　　

　　这个表达式反映了斜面面积，射影面积以及这两个平面所成的二面角之间的关系，并且可以推广到任意的平面多边形.在求二面角的平面角有困难时，可借助此关系式求.

例：如图，M为正方体ABCD－A1B1C1D1的棱AA1的中点，求截面DMB1与底面ABCD所成二面角的大小.

分析一：

　　题中平面DMB1与平面ABCD只给出了一个公共点，要作出二面角的平面角，须先作出二面角的棱.

解法一：

　　设截面DMB1与底面的交线为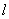，则D∈.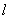

　　取CC1的中点为N，则MN∥AC，∴ MN∥平面AC.

　　易证B1MDN四点共面，且MN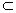平面B1MDN，平面B1MDN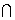平面ABCD=，

　　

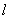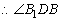　　为二面角B1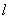－－β的平面角.

　　∵cos∠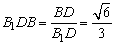，∴∠B1DB=arccos.

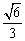　　即截面DMB1与底面ABCD所成角为arccos.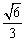

分析二：

　　由于△DMB1在底面ABCD上的射影是△DAB，可考虑用二面角的α的射影公式.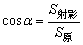

解法二：

　　∵△DMB1在底面ABCD上的射影为△DAB，设所求的二面角为α，

　　正方体棱长为a，又S△DAB=，，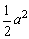

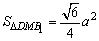　　∴cos.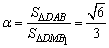

　　即截面DMB1与底面ABCD所成二面角为.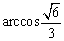

评析：

　　（1）对于未给棱的二面角求法，一般情况下，首先作棱，在有利条件下，利用射影公式求解更方便，射影面积公式为.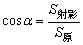

　　（2）本例解法一也可通过延长B1M交BA的延长线于F，则DF为二面角的棱，然后再利用三垂线定理寻找平面角，请同学们自己完成.

-END-