证明两个平面平行要注意线线平行、线面平行与面面平行的相互关系,在高考题中往往与其它知识点结合命题。
证明两个平面平行的方法:①据定义证明两个平面没有公共点,用反证法完成;②据判定定理,证明一个平面内两条相交直线平行于另一个平面;③据“垂直于同一条直线的两个平面平行”,证明两个平面和同一条直线垂直等.
解答或证明前面的有关问题,常常要作辅助线或辅助面,注意两点:一是所作的辅助线或面需要有理论根据;二是辅助线或辅助面具有什么性质,一定要以某一性质定理为依据决不能随意添加.
例、如图所示,在正方体ABCD—A1B1C1D1中,M、N、P分别是C1C、B1C1、C1D1的中点.

求证:(1)AP⊥MN;(2)平面MNP∥平面A1BD.
分析:(1)找出AP在面BB1C1C上的射影,利用三垂线定理证明.
(2)由于M、N、P都为中点,故添加B1C、B1D1作为联系的桥梁.
解:(1)证明:连BC1、B1C,则B1C⊥BC1,BC1是AP在面BB1C1C上的射影.
∴AP⊥B1C,又B1C∥MN,∴AP⊥MN.
(2)证法1:连结B1D1,B1C.
∵P、N分别是D1C1、B1C1的中点,∴PN∥B1D1.
又B1D1∥BD,∴PN∥BD.
又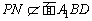 ,∴PN∥平面A1BD. ,∴PN∥平面A1BD.
同理MN∥平面A1BD,又PN∩MN=N,
∴平面PMN∥平面A1BD.
证法2:连AC1,AC,
如图,

∵ABCD—A1B1C1D1为正方体,
∴AC⊥BD.
又CC1⊥面ABCD,
∴AC为AC1在面ABCD上的射影,∴AC1⊥BD.
同理可证AC1⊥A1B,
∴AC1⊥平面A1BD.
同理可证AC1⊥平面PMN,
∴平面PMN∥平面A1BD.
点评:
(2)的证明体现了证明面面平行的两种常用的方法,解决此类问题关键是选择或添加适当的辅助线.
|