多面体是高考立体几何的主要内容，有关棱柱的知识和考查在高考中是重点，每年都有．考查的方向有角度，距离问题，有侧面积、体积等问题．通过棱柱来综合考查线和平面的有关问题．

例1、（全国）如图，直三棱柱ABC－A1B1C1中，∠ACB=90°，AC=1，侧面AA1B1B的两条对角线交点为D，B1C1的中点为M。

　　(1)求证：CD⊥平面BDM；

　　(2)求面B1BD与面CBD所成二面角的大小。

分析：

　　（1）根据直线垂直平面的判定方法证明CD垂直于平面BDM内的两条相交直线，由条件知可证CD⊥DB，CD⊥DM。

　　（2）求面B1BD与面CBD所成二面角先找二面角的平面角，再求平面角。

解答：（1）证明：如图，联结CA1、AC1、CM，则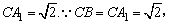

　　　　　 ∴△CBA1为等腰三角形，又知D为A1B的中点，

　　　　　∴CD⊥A1B，∵A1C1=1，.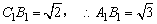

　　　　　又BB1=1，∴A1B=2.

　　　　　∵△A1AB为直角三角形，D为A1B的中点，

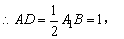　　　　　AD=CC1。

　　　　　又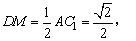DM=C1M，

　　　　　∴△CDM≌△CC1M，∠CDM=∠CC1M=90°，即CD⊥DM。

　　　　　∵A1B、DM为平面BDM内两条相交直线，∴CD⊥平面BDM；

　　　(2)解：设F、G分别 BC、BD的中点，联结B1G、FG、B1F，则FG∥CD，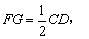

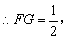　　　　　　FG⊥BD。由侧面矩形BB1A1A对角线的交点为D知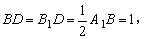

　　　　　　∴△BB1D是边长为1的正三角形，∴B1G⊥BD，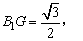

　　　　　　∴∠B1GF是所求二面角的平面角。又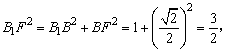

　　　　　　

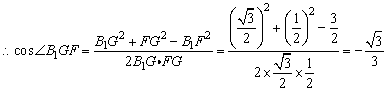
　　　　　　即所求二面角的大小为。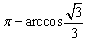

例2、（全国高考题）已知正四棱柱ABCD—A1B1C1D1中，AB=1，AA1=2，点E为CC1的中点，点F为BD1的中点．

　　（1）证明：EF为BD1与CC1的公垂线；

　　（2）求点D1到面BDE的距离．

分析：理清正棱柱的性质，由其中线面关系来解题．

解答：（Ⅰ）取BD的中点M，连MC，MF，

　　　　　　则FMDD1，又CEDD1，CE⊥CM，

　　　　　　∴四边形FMCE为矩形，即EF⊥CC1．

　　　　　　又FE⊥FM，FE⊥DB，∴ FE⊥面BDD1

　　　　　　∴ EF⊥BD1

　　　　　　∴ EF为CC1与BD1的公垂线．

　　　（Ⅱ）连结ED1有：

　　　　　　设D1到面BDE的距离为d ，

　　　　　　

　　　　　　BC=1

　　　　　　∴

　　　　　　即点D1到面BDE的距离为

-END-