|
一、选择题(本题共12小题,每小题5分,共60分,在每小题后给出的四个选项中,只有一项是符合题目要求的.)
1、已知集合I={四棱柱},M={平行六面体},N={直平行六面体},P={正四棱柱},Q={长方体},R={直四棱柱},S={正方体},则下列关系中不正确的是( )
A.S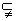 P P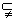 Q B. Q B.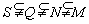
C.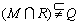 D. D.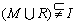
2、正方体的一条对角线与任一个面所成角的正弦值为( )
A.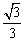 B. B.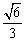
C.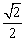 D. D.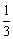
3、长方体的长、宽、高的和为14,对角线长为8,则它的全面积为( )
A.64 B.196
C.132 D.128
4、一棱锥被平行于底面的平面所截,若截面与底面的面积之比为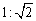 ,一条侧棱被分成的两段之比为( ) ,一条侧棱被分成的两段之比为( )
A.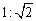 B.1︰2 B.1︰2
C.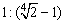 D.1︰1 D.1︰1
5、在正三棱锥S-ABC中,与侧棱SA垂直的棱中一定有( )
A.SB B.SC
C.BC D.AC
6、正四棱锥的底面外接圆半径为10cm,斜高为12cm,则有( )
A.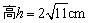
B.侧棱长l=12cm
C.各侧面积之和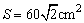
D.两对角面面积之和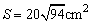
7、正四棱锥P-ABCD的两个侧面PAB与PCD互相垂直,则相邻两个侧面所成二面角的平面角为( )
A.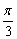 B. B.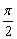
C.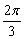 D. D.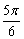
8、在长方体交于一点的三条棱上各取一点,过这三点作一截面,将长方体截去一个角,那么这个截面是( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.以上三种均有可能
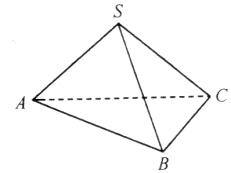
9、如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值为( )
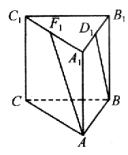

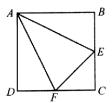
10、如图,正方形ABCD的边长为1,E、F点分别为BC、CD的中点,沿AE、EF、AF折成四面体,使B、C、D三点重合,则其体积是( )

11、若四面体的一条棱长是x,其余棱长都是1,体积为F(x),则函数F(x)在定义域上( )
A.是增函数但无最大值
B.是增函数且有最大值
C.不是增函数且无最大值
D.不是增函数但有最大值
12、ABCD是边长为a,∠A=60°的菱形,H、G、E、F分别在DA、DC、BA、BC上,且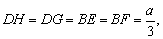 沿HE、FG把两个锐角折起来,使A、C两点重合,这时A到平面EFGH的距离为( ) 沿HE、FG把两个锐角折起来,使A、C两点重合,这时A到平面EFGH的距离为( )
[提示]
二、填空题(本大题共4个小题,每小题4分,共16分,把正确答案填在题中横线上.)
13、正n棱柱每相邻两个侧面之间的二面角的度数是_______.
14、正四棱锥的底面边长为a,高为h,则过侧棱和高所作的截面的面积是________.
15、已知点P是棱长为1的正四面体ABCD内的任意一点,点P到该正四面体四个面的距离分别为h1、h2、h3、h4,则h1+h2+h3+h4等于___________.
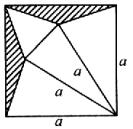
16、如图,将边长为a的正方形剪去如图所示的阴影部分,沿图所画的线折成一个正三棱锥,则这个正三棱锥的高为________.
[答案]
三、解答题(本大题共6小题,前5小题每小题12分,最后1小题14分,共74分,解答应写出必要的文字说明,证明过程或演算步骤.)
17、如图,已知P是△ABC所在平面外的一点,PA、PB、PC两两垂直,且PA=PB=PC=3.求点P到平面ABC的距离.
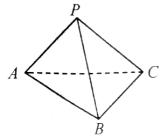
[答案]
18、如图,在三棱锥S-ABC中,侧面SAC⊥底面ABC,△SAC是边长为4的等边三角形,∠ACB=90°,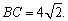
(1)求证:面SAC⊥面SBC;
(2)求SB与面ABC所成的角.
[答案]
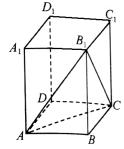
19、如图,已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为
(1)求二面角B1—AC—B的大小;
(2)求点B到平面AB1C的距离.
[答案]
20、如图,在□ABCD中,∠A=60°,AD=1,AB=2,点M和点N分别为DC和AB的中点,以MN为棱将□ABCD折成60°的二面角A—MN—C′,其中A、D的位置不动,B、C到B′、C′.
(1)求证:MN⊥B′D;
(2)求三棱柱AB′N—DC′M的侧面积.

[答案]
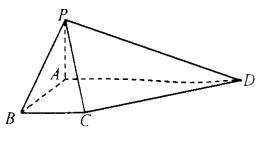
21、如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AB=a,AD=3a,且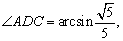 PA⊥平面ABCD,PA=a. PA⊥平面ABCD,PA=a.
(1)求二面角P—CD—A的大小;
(2)求点D到平面PBC的距离.
[答案]
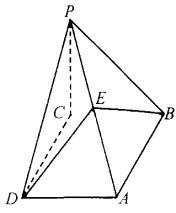
22、如图,四棱锥P-ABCD的底面是边长为1的菱形,∠ABC=60°,PC⊥平面ABCD,PC=1,E为PA的中点.
(1)求证:平面EDB⊥平面ABCD;
(2)求点E到平面PBC的距离;
(3)求二面角A—EB—D的正切值.
[答案]
|