两条直线的位置关系，是解析几何的基础，同时本部分内容所涉及到“数形结合”，“对称”、“化归”等方法也是解析几何的重要思想方法，在历年的高考试题中，本部分内容也是常考问题的热点之一，多以选择题、填空题形式出现，也与圆锥曲线内容及代数有关问题有关知识结合一起命题，成为试卷中的中等题和难题．

例1、（黄冈）点C(a, b)(ab≠0)是一个定点，过C作两条互相垂直的直线l1与l2，若l1交x轴于点A，l2交y轴于点B.

（1）求线段AB 的中点M 的轨迹方程；

（2）若|MC|的最小值为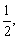求a、b满足的关系式.

解析：（1）当l1与坐标轴不垂直时，设l1︰y－b=k(x－a)，

　　　　则

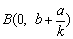
　　　从中消去参数k得2ax＋2by－(a2＋b2)=0，

　　　当l1与坐标轴垂直时动点坐标也适合，

　　　故得所求的中点M的轨迹方程是2ax＋2by－(a2＋b2)=0.

　　　（2）|MC|的最小值即是C点到M点的轨迹的距离，由点到直线的距离公式得

　　　|MC|min=，∴a2＋b2=1为所求的关系式.

例2、（上海）a=3是直线ax＋2y＋3a=0和直线3x＋(a－1)y=a－7平行且不重合的（　）

A、充分非必要条件

B、必要非充分条件

C、充要条件

D、既非充分，也非必要条件

答案：C

解析：由.

例3、（上海）设a，b，c分别是△ABC中∠A，∠B，∠C所对应的边长，则直线xsinA＋ay＋c=0与直线bx－ysinB＋sinC=0的位置关系是（　）

A、平行　　　　　　　　　　B、重合

C、垂直　　　　　　　　　　D、相交但不垂直

分析：本题从判断两直线垂直的方法入手，主要根据斜率关系判定位置关系，但要结合三角形的边角关系，使问题得以解决．

解答：设三角形ABC外接圆半径为r．

　　　由题意知a≠0，sinB≠0，

　　　直线的斜率分别是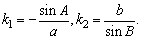

　　　由正弦定理得：

　　　

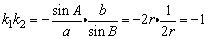
　　　故两条直线垂直，故选C．

-END-