圆锥曲线是高考重点考查的内容，每年都有一道解答题，这类试题特点主要有，求动点的轨迹方程，求指定的圆锥曲线的方程，对称问题或直线与圆锥曲线的有关问题等．这类试题有时计算量较大，难度较大，应注意运用数形结合思想，函数与方程的思想等分析解决．涉及抛物线的问题在高考中时有出现，由于抛物线相对较为简单，故试题相对会容易一些，应注意定义的运用．

例1、（高考，全国卷III）设A(x1, y1), B(x2, y2)两点在抛物线y=2x2上，是AB的垂直平分线．

（1）当且仅当x1＋x2取何值时，直线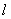经过抛物线的焦点F？证明你的结论；

（2）当直线的斜率为2时，求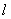在y轴上截距的取值范围．

分析：

　　（1）A，B两点与准线的距离相等即两点纵坐标相等；（2）利用方程的根的判别式和A，B的中点求解．

解：

　　（1）A、B两点到抛物线的准线的相等，

　　∵抛物线的准线是x轴的平行线，y1≥0, y2≥0，

　　依题意y1, y2不同时为0，∴上述条件等价于

　　；

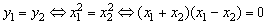　　∵x1≠x2，

　　∴上述条件等价于x1＋x2=0．即当且仅当x1＋x2=0时，经过抛物线的焦点F．

　（2）设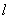在y轴上的截距为b，依题意得的方程为y=2x＋b；

过点A、B的直线方程可写为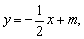

所以x1，x2满足方程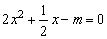

A，B为抛物线上不同的两点等价于上述方程的判别式

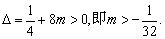
设AB的中点N的坐标为(x0, y0),则

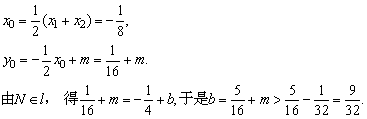
即得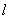在y轴上截距的取值范围为

例2、（全国高考题）如图所示，直线l1和l2相交于点M，l1⊥l2，点N∈l1，以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等，若△AMN为锐角三角形，|AM|=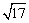，|AN|=3，且|BN|=6，建立适当的坐标系，求曲线段C的方程.

分析：

　　因为曲线段C上的任一点到l2的距离与到点N的距离相等．根据抛物线定义知，曲线段C为以N为焦点，以l2为准线的抛物线的一段，所以本题关键是建立适当坐标系，确定C所满足的抛物线方程.

解：以l1为x轴，MN的中点为坐标原点O，建立直角坐标系.

　　由题意，曲线段C是以N为焦点，以l2为准线的抛物线的一段，其中A、B分别为曲线段的两个端点．

　　∴ 设曲线段C所满足的抛物线方程为y2=2px（p＞0）（xA≤x≤xB，y＞0），其中xA、xB为A、B的横坐标.

　　令|MN|=p，则M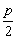（－，0），N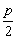（，0）.

　　∵ |AM|=，|AN|=3，

　　∴ 由两点间的距离公式，得方程组

　　解得

　　∵ △AMN为锐角三角形，

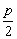　　∴ ＞xA. 则p=4，xA=1.

　　又B在曲线C上，∴ .

　　则曲线段C的方程为y2=8x（1≤x≤4，y＞0）.

例3、（全国高考试题）设抛物线y2=2px（p＞0）的焦点为F，经过点F的直线交抛物线于A、B两点，点C在抛物线的准线上，且BC∥x轴，证明直线AC经过原点O.

分析：

　　问题即为A、O、C三点共线，可考虑CO的斜率等于OA的斜率，本题证明方法很多，这里仅就这一思路证明.

解答：

　　设直线AB的方程为，代入抛物线方程得y2－2mpy－p2=0.

　　记A（x1，y1），B（x2，y2），则y1、y2是方程的两个根.

　　y1y2=－p2，因为BC∥x轴，且点C在准线x=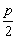－上，

　　所以点C的坐标为（－，y2）.

　　∴ ．

　　∴ A、O、C三点共线，即直线AC经过原点O．

-END-