1、课本P119习题8.5第七题：过抛物线y2=2px的焦点的一条直线和抛物线相交，两个交点的纵坐标为y1、y2，求证：y1y2=－p2．
下面是此题的几个变式，你能否试着去解决？
证明：
在本题中，直线AB过焦点F1，具有上述性质，反之若直线与抛物线y2=2px的两个交点的纵坐标y1、y2具有y1·y2=－p2，直线是否经过焦点F呢？
变式1：若抛物线y2=2px上两个动点A、B的纵坐标分别是y1、y2且满足y1y2=－p2，则直线AB经过焦点F.
证明：
设A、B的坐标分别为(x1，y1)、(x2，y2).
若x1=x2，则由y12=2px1，y22=2px2，知y12=y22，
所以|y1|=|y2|=p，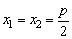
，此时直线AB过焦点F.
若x1≠x2，由直线的斜率公式得
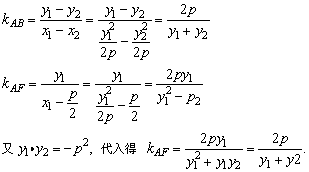
∴ kAF=kAB，因此A、F、B三点共线，直线AB过焦点F.
即y1y2=－p2是AB过焦点F的充要条件．
变式2：
设M（a，0）是抛物线y2=2px对称轴上的一个定点，过M的直线交抛物线于A、B两点，其纵坐标为y1、y2，求证y1y2是定值.
证明：
因为AB与抛物线交于两点，因此可设AB的方程为x=my＋a代入y2=2px中消去x得：y2－2pmy－2pa=0，由韦达定理知y1y2=－2pa（定值）．
变式3：
设抛物线y2=2px上面动点A、B分别为（x1，y1），（x2，y2），且满足y1y2=k（k为常数），问AB是否恒过某一定点？
解：
当x1≠x2时，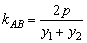
，
AB的方程为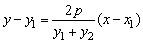
.
将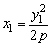
代入化简，整理得
.
∵ y1y2=k，∴ AB的方程为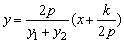
，
即AB过定点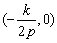
.
当x1=x2时，结论成立，（实际上k≥0时，y1、y2同号，点A、B在对称轴的同侧且x1≠x2，所以当x1=x2时，必有k＜0.）
变式4：
设抛物线y2=2px的两动点A（x1，y1），B（x2，y2），满足y1y2=k（k是常数），求AB中点P的轨迹方程．
解：
设P的坐标为（x，y），则
又A、B在抛物线上，所以有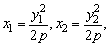
则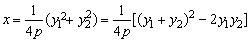 
，
将y1＋y2=2y，y1y2=k代入化简得点P的轨迹方程是
由以上可知，对课本题进行联想、引申和改造，可以得到综合性强，形式新颖的命题，多思考、多训练可提高思维的广阔性与灵活性，培养探索创新的能力．
