|
第I卷(选择题共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题后给出的四个选项中,只有一项是符合题目要求的.)
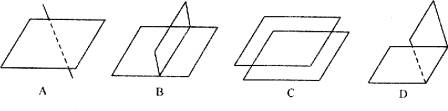
1、下列画法正确的是( )
2、如果两条异面直线称为“一对”,那么在正方体的12条棱中,共有异面直线( )
A.12对 B.24对
C.36对 D.48对
3、如图所示,ABCD-A1B1C1D1是正方体, 则BE1与DF1所成的角的余弦值是( ) 则BE1与DF1所成的角的余弦值是( )

A. B. B.
C.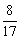 D. D.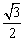
4、已知a、b是平面α外的两条直线,a∥α的前提条件下,“a∥b”是“b∥α”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5、直线a、b是异面直线,a∥平面α,则b与α的位置关系是( )
A.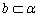 B.b∥a B.b∥a
C.b与a相交 D.以上均有可能
6、若一直线上有两点到一平面内某一直线的距离相等,则直线与平面的位置关系是( )
A.平行 B.相交
C.在平面内 D.以上均有可能
7、a、b是异面直线,A是不在a、b上的点,则下列结论中正确的是( )
A.过A且平行于a、b的平面可能不存在
B.过A且平行于a、b的平面存在且惟一
C.过A且平行于a、b的平面存在但不惟一
D.过A且平行于a、b的平面一定不存在
8、直线l及l外两点A、B,下列说法中正确的是( )
A.过A、B有惟一平面与直线l平行
B.过A、B没有平面与直线l平行
C.过A、B有无数个平面与l平行
D.以上说法都不对
9、AB、CD是夹在两平行平面α、β之间的异面线段,A、C在α内,B、D在β内.若M、N分别为AB、CD的中点,则有( )
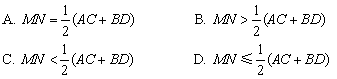
10、已知AB、CD是夹在两平行平面α、β之间的两条线段,AB⊥AC,AB=2,AB与平面β成30°角,则线段AC的范围是( )

11、从正方体的棱和各个面上的对角线中选出R条,使得其中任意两条线段所在的直线都是异面直线,则R的最大值为( )
A.2 B.3
C.4 D.5
12、在△ABC中,∠C是直角,平面ABC外有一点P,PC=4cm,点P到直线AC,BC的距离都等于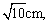 那么PC与平面ABC所成的角的大小为( ) 那么PC与平面ABC所成的角的大小为( )
A.30° B.45°
C.60° D.75°
[提示]
第II卷(非选择题共90分)
二、填空题(本大题共4个小题,每小题4分,共16分,把正确答案填在题中横线上.)
13、正方体的截面多边形的边数可能是_________________.
14、如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的点,它们共面,并且AC∥平面EFGH,BD∥平面EFGH,AC=m,BD=n,当EFGH是菱形时,AE︰EB=_______.
15、下列命题中:①若两条直线没有公共点,则这两条直线平行;②若两条直线没有公共点,则这两条直线异面;③若两条直线都和第三条直线平行,则这两条直线平行;④若两条直线都和第三条直线相交成等角,则这两直线平行.正确命题的序号是___________.
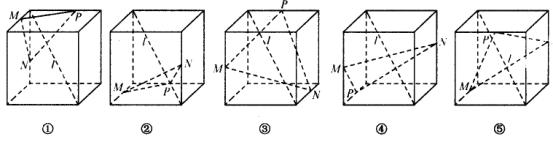
16、如图中,五个正方体图形,l是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出l⊥面MNP的图形的序号是___________.(写出所有符合要求的图形序号)
[答案与解析]
三、解答题(本大题共6小题,前5小题每小题12分,最后1小题14分,共74分,解答应写出必要的文字说明,证明过程或演算步骤.)
17、一个平面可以将空间分成几个部分?两个平面可以将空间分成几个部分?三个平面又可将空间分成几个部分?
[答案]
18、设a和b是两条异面直线.求证:
(1)过a和b分别存在平面α和β,使得α∥β;
(2)在条件(1)中α和β间的距离即是异面直线a和b间的距离.
[答案]
19、已知A1、B1、C1和A2、B2、C2分别是异面直线l2和l1上的任意不同的三点,M、N、R、T分别是A1A2、B1A2、B1B2、C1C2的中点.求证:M、N、R、T四点共面.
[答案]
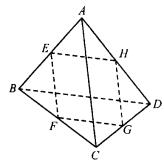
20、如图所示,A点是△BCD所在平面外的一点,∠ABD=∠ACD=90°,AB=AC,E是BC的中点.
(1)求证:AD⊥BC;
(2)试判断△ADE的形状,并证明你的判断.

[答案]
21、如图所示,△ABC与△A′B′C′的对应顶点的连线AA′、BB′、CC′交于同一点O,且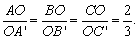
(1)证明:AB∥A′B′,AC∥A′C′,BC∥B′C′;
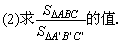
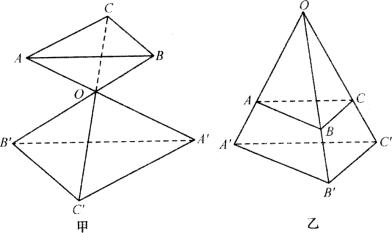
[答案]
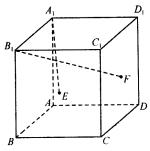
22、如图的正方体ABCD-A1B1C1D1中,E、F分别是相邻两个侧面BCC1B1和CDD1C1的中点.
(1)判断直线A1E与B1F的位置关系;
(2)求A1E和B1F所成的角.
[答案]
|