A、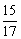 B、
B、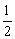 C、
C、 D、
D、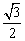
分析:本题考查了空间异面直线所成的角,解三角形知识.
解答:
过A点在平面ABB1A1内作AF,使A1F=D1F1,则四边形ADF1F是平行四边形.
∴ AF∥DF1,再过E1在平面ABB1A1内作E1E∥FA
则 ∠BE1E即BE1与DF1所成角或其补角.
由已知 B1E=D1F1=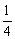 A1B1
A1B1
∴ BE1=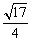 A1B1,又DF1=AF=E1E,
A1B1,又DF1=AF=E1E,
而 DF1=BE1,∴ E1E=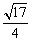 A1B1,
A1B1,
显然,EB= A1B1,在△BE1E中,由余弦定理cos∠BE1E=
A1B1,在△BE1E中,由余弦定理cos∠BE1E=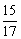 .
.
故选A.
答案:A
例2、(全国高考试题)在棱长都相等的四面体A—BCD中,E、F分别是棱AD、BC的中点,连结AF、CE,如图所示,求异面直线AF、CE所成的角的余弦值.