高考中对“球”的考查要求是了解球的概念，掌握球的性质，掌握球的表面积、体积公式．球的有关计算高考一般以客观题的形式出现，主要考查球的性质，面积和体积的计算，难度不大，所以应以基本概念和基本运算为主．

例1、(全国卷Ⅰ)一个与球心距离为1的平面截球所得的圆面面积为π，则球的表面积为(　　)

解析：

　　∵截面圆面积为，∴截面圆半径，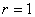

　　∴球的半径为，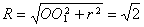

　　∴球的表面积为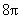，故选B．

答案：B

点拨：找相关的直角三角形．

例2、(全国卷Ⅱ)将半径都为1的4个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最小值为(　)

　　　

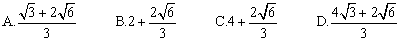
解析：

　　易知当三个球两两相切在底层，而另一个球在三个球上面与三球相切时高最小．如图，设正四面体为ABCD，四个球心分别为O1，O2，O3，O4，则AO1⊥面BCD，而面O2O3O4∥面BCD．由O1O2O3O4是正四面体，且O1O2=2，易得O1O=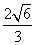＋1．设球O1与面ACD切于点F，连AF并延长交CD于E，连OE，则△AFO1∽△AOE，

　　∴，

　　∴AO=4＋，即正四面体的高最小值为4＋．

答案：C

-END-