在求球的体积与表面积时，都用到了分割，以直代曲，聚零为整，求近似值，变有限为无限，化近似和为准确和等思维方法．下面我们用类似方法解决这类问题．
椭圆绕着它的一条轴旋转一周（半周亦可）所得的几何体叫做椭球，或者空间与两个定点F1，F2的距离的和等于或小于常数（大于| F1F2|）的点的轨迹叫做椭球．
设椭球是由长半轴长为a，短半轴长为b的椭圆绕其短轴所在直线旋转得到，试用a,b表示该椭球的体积．
解：如图为半椭球，在yOz平面内，半椭圆ABC的方程为
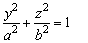（a>b>0,z≥0） ①
把OA作n等分，经过这些分点，用一组平行于底面的平面把半椭球切割成n层，每一层都近似于一个圆柱形的“薄圆片”，这些“薄圆片”的体积之和就是半椭球的体积.
这些圆柱的高就是“薄圆片”的厚度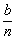
，底面就是“薄圆片”的下底面.由方程①知，第二层（由下向上数）“薄圆片”的下底半径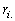
满足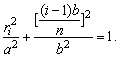
∴
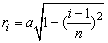，i=1,2,…,n.
于是第i层“薄圆片”的体积是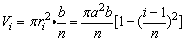
，i=1,2,…,n.
半椭球的体积是
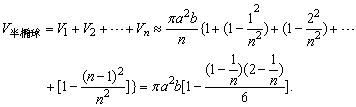②
容易看出，当所分层数不断增加，也就是n不断变大时，②式的精确程度越来越高．如果n变为无穷大，那么就能由②式推出V半椭球的准确值．随着n的增大，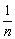
越来越小，当n变得无穷大时，
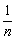趋近于0.这时就能由②式推得
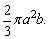V半椭球=
∴V椭球=
