一、圆系与圆系问题
具有某种共同性质的圆的集合,称为圆系.几种常见的圆系方程有:
1°同心圆系: (x-x0)2+(y-y0)2=r2(x0,y0为常数,r为参数)
2°圆心共线的半径相等的圆系:
(x-x0)2+(y-y0)2=r2(r为常数,圆心(x0,y0)在直线ax+by+c=0上移动)
3°过两已知圆C1∶x2+y2+D1x+E1y+F1=0,C2∶x2+y2+D2x+E2y+F2=0 的交点的圆系方程:
x2+y2+D1x+E1y+F1+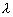 (x2+y2+D2x+E2y+F2)=0 (x2+y2+D2x+E2y+F2)=0
4°过直线与圆交点的圆系方程:
设直线l∶Ax+By+c=0与圆C∶x2+y2+Dx+Ey+F=0相交,则方程x2+y2+Dx+Ey+F+λ(Ax+By+c)=0表示过直线l与圆C的两个交点的圆系方程.
例题:已知圆C的半径为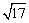 ,圆心在直线x-y-2=0上,且过点(-2,1),求圆C的方程. ,圆心在直线x-y-2=0上,且过点(-2,1),求圆C的方程.
解: ∵圆心在直线x-y-2=0上,且r=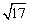 , ,
∴设圆心为(t, t-2)(t为参数),
∴圆C的方程为:(x-t2)+(y+2-t)2=17,
∵圆C过点(-2,1) ,
∴(-2-t)2+(1-t+2)2=17,
解得 t=2,或t=-1,
∴圆心C的坐标是(2,0)或(-1,-3).
∴所求圆C的方程是:(x-2)2+y2=17或(x+1)2+(y+3)2=17.
同学们不妨利用圆系知识解决如下问题:
已知圆在x轴上两个截距分别为a,b,在y轴上的一个截距为c(c≠0), 试求此圆的方程.
二、切点弦方程
问题1:过圆x2+y2=r2外一点M(x0,y0),作这个圆的两条切线MA、MB,切点分别是A、B,求直线AB的方程(直线AB称作切点弦).
解:
如图所示,设切点A的坐标为(x1,y1),切点B的坐标为(x2,y2).
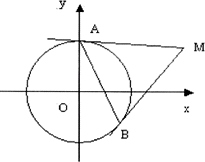
因为圆的方程为x2+y2=r2 ①
所以过圆上一点A(x1,y1)所作的切线的方程为x1x+y1y=r2 ②
由于M(x0,y0)在直线AM上,所以x1x0+y1y0=r2 ③
同理,根据点M在切线BM上,得x2x0+y2y0=r2 ④
③④表明,点A(x1,y1)和点B(x2,y2)都在下面的直线上x0x+y0y=r2 ⑤
因为过两点只有一条直线,所以⑤就是直线AB的方程.
即点M的切点弦方程为:x0x+y0y=r2.
问题1解法的基本思想是设而不求.设了点A和点B的坐标,但是不求出这些坐标,只是借用它们的形式,把最终的问题解决.
从问题1中,我们不仅学习了切点弦方程,还学习了设而不求的解题思想.下面看一个与之相关的问题.
问题2:设M(x0,y0)是圆x2+y2=r2内的一点,但不是圆心.过点M任意作两条不通过圆心的弦AB和CD,分别过点A、B作圆的切线相交于点P,过点C、D作圆的切线相交于点Q,求直线PQ的方程.
解:如图,设点P的坐标为(x1,y1),点Q的坐标为(x2,y2),因为圆的方程是x2+y2=r2 ①
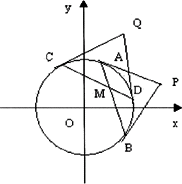
PA、PB是过圆外一点所作圆的切线,A、B是切点,所以切点弦AB的方程为x1x+y1y=r2 ②
同理切点弦CD的方程为x2x+y2y=r2 ③
因为M(x0,y0)在直线AB上,所以x1x0+y1y0=r2 ④
同理M(x0,y0)在直线CD上,所以x2x0+y2y0=r2 ⑤
④⑤表明点,点P(x1,y1)和点Q(x2,y2)都在下面的直线上x0x+y0y=r2 ⑥
因为过两点只有一条直线,所以⑥就是直线PQ的方程.
不难看出,上述两个问题的紧密联系,同样是用设而不求的思想方法,问题2还运用了问题1的结论,更为有趣的是二者其实还是一个问题的两个方面,具体如下:
一般地,已知圆x2+y2=r2和平面内的任意点M(x0,y0),只要M不是圆心(0,0),总可以作出对应的直线m:x0x+y0y=r2.这样得到的直线m叫做点M关于圆的极线(当M在圆外时,m也叫切点弦),点M叫作直线m的极点.
问题1是点M在圆外时的情况,问题2是点M在圆内时的情况,并且同时也给出了作相应极线的几何作图方法.当然,点M在圆上时,它的极线就是过点M的圆的切线.三种情况的极线方程都是x0x+y0y=r2,这种高度的统一性真是妙不可言.其实极点、极线的概念就是切点、切线概念的推广,它们还有很多重要的性质,高等几何中里有详细研究.
|