双曲线的方程和性质，高考试题中常考常新，常常是双曲线方程与直线的小综合的选择题或填空题，属于中档题目。解答题中以双曲线与直线等知识大型综合试题为主，难度中等偏上，考查综合运用知识、分析解决问题的能力．

例1、（湖南）已知双曲线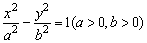的右焦点为F，右准线与一条渐近线交于点A，△OAF的面积为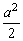（O为原点），则两条渐近线的夹角为（　）

A．30°　　　　B．45°　　　　　C．60°　　　　　　D．90°

答案：D

解答：设渐近线为，则A的纵坐标，

　　　

　　　∴双曲线为等轴双曲线，

　　　∴两渐近线夹角为90°。

例2、（浙江）已知双曲线的中点在原点，右顶点为A（1，0），点P、Q在双曲线的右支上，点M（m，0）到直线AP的距离为1，

　　（1）若直线AP的斜率为k，且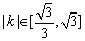，求实数m的取值范围；

　　（2）当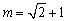时，△APQ的内心恰好是点M，求此双曲线的方程。

分析：本题综合性强，第一问通过直线与双曲线关系就可解决，第二问实际是用待定系数法求双曲线方程。

解答：（1）由条件得直线AP的方程y=k(x－1),

　 　　　　即kx－y－k=0。

　　　　　 因为点M到直线AP的距离为1，

　　　　　

　　　

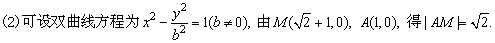
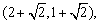　　又因为M是△APQ的内心，M到AP的距离为1，所以∠MAP=45°，直线AM是∠PAQ的角平分线，且M到AQ、PQ的距离均为1，因此，kAP=1, kAQ=－1（不妨设P在第一象限），直线PQ方程为直线AP的方程y=x－1，解得P的坐标是将点P坐标代入所以所求双曲线方程为

点评：本题字母涉及多，直线与双曲线的关系运算处理较繁，这里要格外注意。

例3、（全国理）已知l1、l2是过点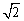（－，0）的两条互相垂直的直线，且l1,l2与双曲线y2－x2=1各有两个交点，分别为A1、B1和A2、B2.

　　（1）求l1的斜率k1的取值范围；

　　（2）若|A1B1|=|A2B2|，求l1,l2的方程.

分析：

　　设出l1,l2的点斜式方程，由直线与曲线交于两点等价于方程组有两组解可求得k1的范围；由|A1B1|=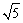|A2B2|结合韦达定理可得k1的方程，求出k1的值.

解答：（1）依题意，l1,l2的斜率都存在，因为l1过点P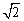（－，0），且与双曲线有两个交点，

　　　　　　故方程组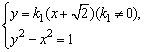　　　①

　　　　　　有两组不同的解.

　　　　　　在方程组①中消去y，整理得：

　　　　　　　　　②

　　　　　　则应有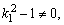

　　　　　　．

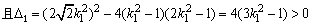　　　　　　同理，设l2的斜率为k2，则方程组

　　　　　　　　　③

　　　　　　有两组不同的解，在方程组③中消去y，整理得

　　　　　　

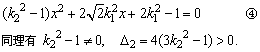
　　　　　　又因为l1⊥l2，所以有k1·k2=－1

　　　　　　于是，l1、l2与双曲线各有两个交点，等价于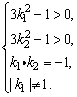

　　　　　　.

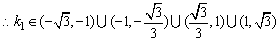　　　　（2）设A1(x1,y1)，B1(x2,y2)，由方程②知

　　　　　　

点评：

　　本题的计算量较大，但由于解答中运用了简算技巧，所以计算量被降低了很多，同时说明高考对大家的运算能力有较高的要求.

-END-