双曲线定义的应用
例1、已知双曲线
的右焦点F，点A（9，2），试在这个双曲线上求一点M，使|MA|＋
|MF|的值最小，并求出这个最小值.
分析：
如何处置|MF|前的系数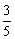
，注意到
恰好是双曲线的离心率，|MF|是双曲线上的点到焦点的距离，考虑到双曲线第二定义，难点化解了．
解答：
如图所示，l为双曲线的右准线，M为双曲线上任意一点，作MN⊥l于N，作AB⊥l于B.
∵ 离心率e=
，∴
由双曲线的第二定义，有
.
∴ |MA|=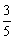
|MF|，∴
|MA|＋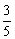
|MF|=|MA|＋|MN|≥AB.
当且仅当M为AB与双曲线右支的交点时，|MA|＋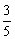
|MF|取得最小值，
此时，点M的坐标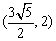为
，最小值为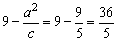
.
例2、已知双曲线
的焦点为F1（－c，0），F2（c，0）（c>0），e为离心率，点P为左支上一点，d为P到左准线的距离．
（1）当|PF1|2=d·|PF2|时，求e的范围.
（2）当2|PF1|=d＋|PF2|时，求e的范围.
分析：
依题设，明显d<|PF1|<|PF2|，d、|PF1|、|PF2|组成等比数列或等差数列的可能性是存在的．
解：
依定义，有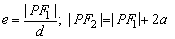
.
（1）由|PF1|2=d·|PF2|得
.
∴ |PF1|=
，∵
P在右支上，∴ |PF1|≥c－a，
即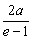 
≥c－a，
∴ 
≥e－1，
即 (e－1)2≤2，∴ e－1≤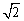
.
又∵ e>1，∴ 1<e<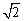
＋1，
即e的取值范围为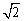（1，
＋1].
（2）由2|PF1|=d＋|PF2|，得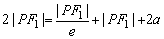
.
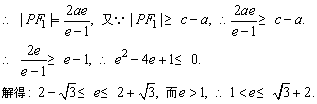
即e的取值范围为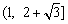
.
对于本单元，要进一步加强对双曲线的定义及有关概念的理解，熟练掌握其标准方程及几何性质．对于双曲线与其它曲线的关系问题，更要多加训练，对于一些实际问题，善于利用数形结合的方法去解决.
例如，已知a>0，a≠1，试求使方程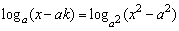
有解的k的取值范围．这是一个解含参数的对数方程的问题，前面我们已利用对参数的讨论，找到原方程的等价条件是
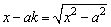>0，下面利用数形结合的方法解答此题.
联系函数的图象考虑，原方程有解的充要条件是函数y=x－ak与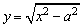
（y>0）的图象有交点，由于
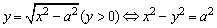（y>0），可知它的图象是等轴双曲线x2－y2=a2的两上半支（顶点除外）．如图，直线y=x－ak与双曲线x2－y2=a2的左上半支有交点的充要条件是－ak>a，即k<－1，而与双曲线的右上半支有交点的充要条件是－a<－ak<0，即0<k<1.
