1、动点P到M(1,0)的距离与到点N(3,0)的距离之差为2,则点P的轨迹是( )
A.双曲线 B.双曲线的一支
C.两条射线 D.一条射线
2、双曲线的两条渐近线的夹角为60°,则双曲线的离心率是( )
A.2或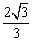 B.2
B.2
C.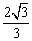 D.
D.
3、如图所示,已知双曲线 的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则此双曲线的离心率e的最大值为( )
的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则此双曲线的离心率e的最大值为( )
A. B.
B.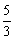
C.2 D.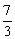
4、设双曲线 (a>0,b>0)的一条准线与两条渐近线交于A、B两点,相应焦点为F,若△ABF为正三角形,则双曲线的离心率为( )
(a>0,b>0)的一条准线与两条渐近线交于A、B两点,相应焦点为F,若△ABF为正三角形,则双曲线的离心率为( )
A.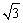 B. 3
B. 3
C.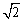 D.2
D.2
5、如图所示,若a、b∈R,ab≠0,则方程ax-y+b=0和bx2+ay2=ab的曲线方程是( )

A.
B.
C.
D.
6、若双曲线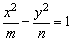 (m>0,n>0)和椭圆
(m>0,n>0)和椭圆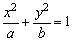 (a>b>0)有相同的焦点F1、F2,M为两曲线的交点,则|MF1|·|MF2|等于( )
(a>b>0)有相同的焦点F1、F2,M为两曲线的交点,则|MF1|·|MF2|等于( )
A.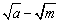 B.a-m
B.a-m
C.a2-m2
D.2(a-m)
7、已知双曲线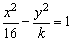 的一条准线恰好为圆x2+y2+2x=0的一条切线,则实数k的值为( )
的一条准线恰好为圆x2+y2+2x=0的一条切线,则实数k的值为( )
A.48 B.42
C.64 D.16
8、直线y=x+3与曲线 ()
()
A.没有交点 B.只有一个交点
C.有两个交点 D.有三个交点
9、直线l过双曲线 的右焦点,斜率k=2,若l与双曲线的两个交点分别在双曲线左、右两支上,则双曲线的离心率e的取值范围是( )
的右焦点,斜率k=2,若l与双曲线的两个交点分别在双曲线左、右两支上,则双曲线的离心率e的取值范围是( )
A.e> B.1<e<
B.1<e<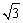
C.1<e< D.e>
D.e>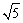
10、双曲线 的离心率为e1,
的离心率为e1,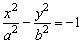 的离心率为e2,其中a>0,b>0,则e1+e2的最小值为( )
的离心率为e2,其中a>0,b>0,则e1+e2的最小值为( )
A.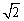 B.2
B.2
C.2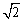 D.4
D.4