椭圆的第一、二定义及几何性质，a、b、c、e四个量的关系，是非常基础，但极其重要的内容，应熟悉各量的含义，做到心中有图，注意数形结合及以前所学的相关知识的综合运用.
圆锥曲线是历年高考的重点、热点内容之一．一般有基本的选择题与填空题2～3道，还必有一道解答题，此题有时为中等难度，但多数情况是难度较大的“拉距离”题、压轴题，对思维能力，思维方法和运算能力要求较高，只有平时从严训练，才能在考试中取得满意的成绩．
例1、（北京）如图，已知某椭圆的焦点是F1（－4，0）、F2（4，0），过点F2并垂直于x轴的直线与椭圆的一个交点为B，且|F1B|＋|F2B|=10.椭圆上不同的两点A（x1，y1）、C（x2，y2）满足条件：|F2A|、|F2B|、|F2C|成等差数列.
（1）求该椭圆的方程；
（2）求弦AC中点的横坐标；
（3）设弦AC的垂直平分线的方程为y=kx＋m，求m的取值范围.
解析：
（1）由椭圆定义及条件知2a=|F1B|＋|F2B|=10，
得a=5，又c=4，
所以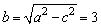
.
故椭圆方程为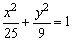
.
（2）由点B（4，yB）在椭圆上，得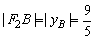
.
解法一：
因为椭圆右准线方程为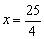
，离心率为
.
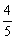根据椭圆定义，有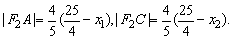
由|F2A|、|F2B|、|F2C|成等差数列，得
.
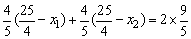由此得出x1＋x2=8.
设弦AC的中点为P（x0，y0），则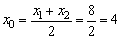
.
解法二：
由|F2A|、|F2B|、|F2C|成等差数列，得
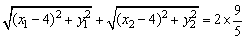①
由A（x1，y1）在椭圆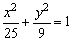
上，
得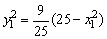
.
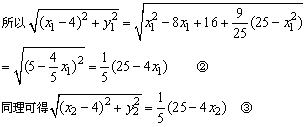
将②、③代入①式，得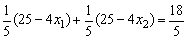
.
所以x1＋x2=8.
设弦AC的中点为P（x0，y0），则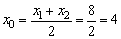
.
（3）解法一：
由A（x1，y1）、C（x2，y2）在椭圆上，
得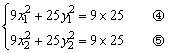
由④－⑤得：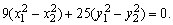
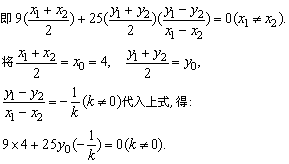
由上式得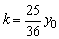 
（当k=0时也成立）．
由点P（4，y0）在弦AC的垂直平分线上，得y0=4k＋m.
所以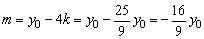
.
由P（4，y0）在线段BB′（B′与B关于x轴对称，如图）的内部，得：
解法二：
因为弦AC的中点为P（4，y0），所以直线AC的方程为：
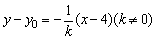⑥
将⑥代入椭圆方程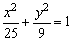
，得
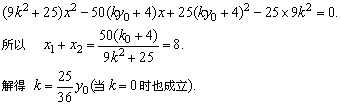
以下步骤同解法一.
评注：
本题考查直线、椭圆、等差数列等基本知识，考查综合运用知识的能力、逻辑推理能力、运算能力、综合性较强．
例2、（全国）已知常数a>0，在矩形ABCD中，AB=4，BC=4a，O为AB的中点，点E、F、G分别在BC、CD、DA上移动，且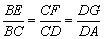
，P为GE与OF的交点（如图所示）．问是否存在两个定点，使P到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由．
解析：
根据题设条件首先求出点P坐标满足的方程，据此可判断是否存在两点，使得点P到两定点距离的和为定值．
按题意，有A（－2，0），B（2，0），C（2，4a），D（－2，4a）.
设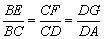
=k（0≤k≤1）.
由此有E（2，4ak），F（2－4k，4a），G（－2，4a－4ak）.
直线OF的方程为：2ax＋(2k－1)y=0. ①
直线CE的方程为：－a(2k－1)x＋y－2a=0 ②
从①、②消去参数k，得点P（x，y）坐标满足方程2a2x2＋y2－2ay=0.
整理得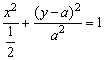
.
当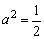
时，点P的轨迹为圆弧，所以不存在符合题意的两点．
当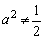
时，点P的轨迹为椭圆的一部分，点P到该椭圆焦点的距离的和为定长．
当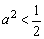
时，点P到椭圆两个焦点
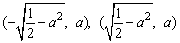的距离之和为定值
.
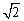当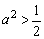
时，点P到椭圆两个焦点
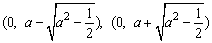的距离之和为定值2a.
评注：
本小题主要考查根据已知条件求轨迹的方法，椭圆的方程和性质，利用方程判定曲线的性质，曲线与方程关系等解析几何的基本思想和综合解题能力．在解题过程中蕴涵着方程思想、分类讨论思想和构造法．
