对于图象的展开与折叠问题，最终还是体现在点、线、面的各种位置关系上，充分体现了对考生的空间想象能力的考查要求．

例1、（高考浙江试题）设M、N是直角梯形ABCD两腰的中点，DE⊥AB于E(如图)．现将△ADE沿DE折起，使二面角A－DE－B为45°，此时点A在平面BCDE内的射影恰为点B，则M、N的连线与AE所成角的大小等于_________．

解：

　　如下图,在平面AED内作MQ∥AE交ED于Q,则MQ⊥ED,且Q为ED的中点,连结QN,则NQ⊥ED且QN∥EB,QN=EB,∠MQN为二面角A－DE－B的平面角,

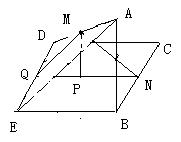
　　∴∠MQN=45°.

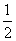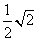　　∵AB⊥平面BCDE,又∠AEB=∠MQN=45°,MQ=AE=EB,

　　在平面MQN内作MP⊥BQ,得QP=MP=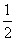EB,故PB=QP=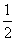EB,

　　故QMN是以∠QMN为直角的等腰三角形,即MN⊥QM,也即MN与AE所成角大小等于90°

例2、（全国高考试题）

　　（1）给出两块面积相同的正三角形纸片（如图①、②），要求用其中一块剪拼成一个正三棱锥的模型，另一块剪拼成一个正三棱柱模型，使它们的全面积与原三角形的面积相等，请设计一种剪拼方法，分别用虚线标示在图①、②中，并作简要说明；

　　（2）试比较你剪拼的正三棱锥与正三棱柱的体积大小；

　　（3）如果给出的是一块任意三角形的纸片（如图③），要求剪拼成一个直三棱柱模型，使它的全面积与给出的三角形的面积相等，请设计一种剪拼方法，用虚线标示在图③中，并作简要说明．

分析：

　　本小题主要考查空间想象能力，动手能力和灵活运用所学知识解决现实问题的能力，从正棱锥、正棱柱的定义出发．

解答：

　　（1）如图④，沿正三角形中点线连线折起，可拼得一个正三棱锥．如图⑤，正三角形三个角上剪出三个相同的四边形，其较长的一组邻边边长为三角形边长的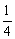，有一组对角为直角，余下部分按虚线折起，可成为一个缺上底的正三棱柱，而剪出的三个相同的四边形恰好拼成这个正三棱柱的上底．

　　（2）依上面剪拼方法，有．

　　设给出的正三角形纸片的边长为2，那么正三棱锥与正三棱柱的底面都是边长为1的正三角形，其面积为，现计算它们的高．

　　

　　（3）如图⑥所示，分别连结三角形的内心与各顶点，得到三条线段，再以这三条线段的中点为顶点作三角形，以新作的三角形为直三棱柱的底面，过新三角形的三个顶点向原三角形三边作垂线，沿六条垂线剪下三个四边形，可以拼成直三棱柱的上底，余下部分按虚线部分折起，成为一个缺上底的直三棱柱，即可得直三棱柱模型．

-END-