|
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)
1、已知点P(2,2)在双曲线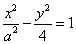 上,则该双曲线的实轴长是( ) 上,则该双曲线的实轴长是( )
A.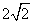 B. B.
C.2 D.4
2、椭圆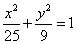 上任意一点P到椭圆两个焦点的距离之差的绝对值的最大值为( ) 上任意一点P到椭圆两个焦点的距离之差的绝对值的最大值为( )
A.10 B.8
C.6 D.4
3、已知抛物线y=mx2(m<0)的焦点到准线的距离是2,则它的焦点坐标是( )
A.(-1,0) B.(-2,0)
C.(0,-1) D.(0,-2)
4、双曲线E过点(2,-2),且与双曲线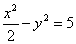 有相同的渐近线,则E的方程是( ) 有相同的渐近线,则E的方程是( )
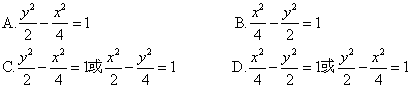
5、设抛物线y2=2px上某三点的纵坐标的平方依次成等差数列,则对应的这三点到抛物线焦点的距离依次所成的数列( )
A.一定是等差数列
B.一定是等比数列
C.既是等差数列也是等比数列
D.既不是等差数列也不是等比数列
6、已知过椭圆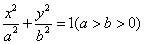 的中心的直线与椭圆交于A,B两点,右焦点为F2(c,0),其中c为半焦距,则△ABF2的最大面积是( ) 的中心的直线与椭圆交于A,B两点,右焦点为F2(c,0),其中c为半焦距,则△ABF2的最大面积是( )
A.ab B.ac
C.b2 D.bc
7、已知双曲线的焦点到渐近线的距离等于右焦点到右顶点的距离的2倍,则此双曲线的离心率e的值为( )
A.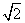 B. B.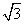
C.2 D.
8、已知椭圆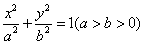 的离心率等于 的离心率等于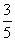 ,将这一椭圆绕它的右焦点按逆时针方向旋转 ,将这一椭圆绕它的右焦点按逆时针方向旋转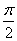 后,所得到的椭圆的一条准线方程是 后,所得到的椭圆的一条准线方程是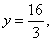 则原来的椭圆方程是( ) 则原来的椭圆方程是( )

9、已知双曲线的方程为 ,过它的一个焦点F1的一条弦AB的长为m,设另一个焦点为F2,则△ABF2的周长为( ) ,过它的一个焦点F1的一条弦AB的长为m,设另一个焦点为F2,则△ABF2的周长为( )
A.2a B.4a-m
C.4a+2m D.4a-2m
10、使方程(5-k)x2+(|k|-2)y2=(5-k)(|k|-2)所表示的曲线是双曲线的实数的集合是M,则这一集合M等价于下列哪个不等式的解集( )

11、已知抛物线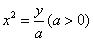 与直线y=kx+b交于两点,它们的横坐标是x1, x2,直线与x轴的交点是x3,那么x1, x2, x3之间的关系是( ) 与直线y=kx+b交于两点,它们的横坐标是x1, x2,直线与x轴的交点是x3,那么x1, x2, x3之间的关系是( )
A.x3=x1+x2 B.x1x2x3= x1+x2
C.x1x2= x1x3+x2x3 D.x1x3= x1x2+x2x3
12、以椭圆上一点和椭圆的两个焦点为顶点的三角形的面积的最大值为1,该椭圆的长轴长也取得最小值,则此时对应的椭圆的准线方程为( )
A.x=±2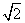 B.x=± B.x=±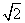
C.x=±4 D.x=±2
[提示]
二、填空题(把正确答案填在题中横线上)
13、到椭圆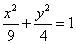 的右焦点的距离是2,到其右准线的距离是______. 的右焦点的距离是2,到其右准线的距离是______.
14、已知抛物线y2=6x,过点(4,1)引抛物线的一条弦,使它恰在该点处被平分,则这条弦所在的直线方程是__________________.
15、若双曲线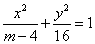 的一条准线方程是 的一条准线方程是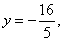 则以(m,0)为圆心且与该双曲线的渐近线相切的圆的方程是_______________. 则以(m,0)为圆心且与该双曲线的渐近线相切的圆的方程是_______________.
16、有下列命题:
①若抛物线y2=2x上两点A,B到焦点的距离之和为5,则线段AB的中点的横坐标是2;
②已知圆x2+y2-6x-7=0与抛物线y2=2px (p>0)的准线相切,则p=1;
③抛物线y2=2px (p>0)的顶点为O点,焦点为F点,若P为此抛物线上一点,则△POF 的形状可能为等边三角形;
④一动圆M 和直线l:x=-2相切,且经过点F(2,0),则动圆圆心的轨迹方程是y2=8x.
其中正确的命题的序号是_________.
[答案]
三、解答题(解答应写出必要的文字说明、证明过程或演算步骤)
17、已知抛物线y2=2px (p>0)有一内接直角三角形,其直角顶点在原点,一直角边所在的直线方程y=2x,若该直角三角形的斜边长为 ,求出这一抛物线的焦点坐标和准线方程. ,求出这一抛物线的焦点坐标和准线方程.
[答案]
18、从椭圆上一点A看两焦点F1、F2的视角为直角,设AF1的延长线交这个椭圆于B,|AB|=|AF2|,求这个椭圆的离心率.
[答案]
19、已知P为双曲线 右支上一点,F1、F2的分别为左、右焦点,若|PF1|︰|PF2|=3︰2,试求P点坐标. 右支上一点,F1、F2的分别为左、右焦点,若|PF1|︰|PF2|=3︰2,试求P点坐标.
[答案]
20、已知双曲线的渐近线方程为3x±2y=0,两准线间距离为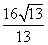 ,求双曲线方程. ,求双曲线方程.
[答案]
21、如图所示,线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线.
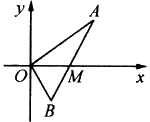
(1)求抛物线方程;
(2)若tan∠AOB=-1.求m的取值范围.
[答案]
22、已知:⊙C过定点A(0,p)(p>0),圆心C在抛物线x2=2py上运动,MN是⊙C在x轴上截得的弦,设|AM|=l1,|AN|=l2,∠MAN=θ.
(1)试问:当点C在抛物线x2=2py上运动时,弦长|MN|是否变化?并证明你的结论;
(2)求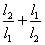 的最大值,以及取最大值时θ的值和⊙C的方程. 的最大值,以及取最大值时θ的值和⊙C的方程.
[答案]
|