|
第Ⅰ卷(选择题,共60分)
一、选择题(本题包括12小题,每小题5分,共60分.在每小题后给出的四个选项中,只有一项是符合题目要求的.)
1、“直线 垂直于平面α内的无数条直线”是“ 垂直于平面α内的无数条直线”是“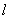 ⊥α“的( ) ⊥α“的( )
A.充分条件 B.必要条件
C.充要条件 D.既不充分也不必要条件
2、将正方体的纸盒展开(如图),直线AB,CD在原正方体中的位置是( )
A.平行 B.垂直
C.相交成60°角 D.异面且成60°角

3、如图所示,正三棱锥V—ABC中,D,E,F分别是VC,VA,AC的中点,P为VB上任意一点,则直线DE与PF所成角的大小是( )
A. B. B.
C. D.随P点的变化而变化 D.随P点的变化而变化
4、如图,空间四边形的各边和对角线长均相等,E是BC的中点,那么( )
A.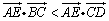 B. B.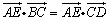
C.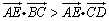 D. D.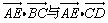 不能比较大小 不能比较大小
5、PQ是异面直线a,b的公垂线,a⊥b,A∈a,B∈b,c在线段PQ上(异于P,Q),则△ABC的形状是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
6、长方体的高等于h,底面积等于Q,垂直于底的对角面的面积是M,则此长方体的侧面积等于( )

7、若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是( )
A.三棱锥 B.四棱锥
C.五棱锥 D.六棱锥
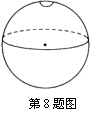
8、如图所示,从放置的球体容器顶部一个孔向球内以相同的速度注水,容器中水面的高度h与注水时间t之间的关系用图象表示应为( )
 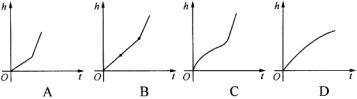
9、已知正方体ABCD—A1B1C1D1的棱长为1,P是AA1的中点,E是BB1上一点,则PE+EC的最小值是( )
A.2 B.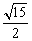
C.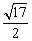 D. D.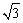
10、如果α∥β,AB和CD是夹在平面α与β之间的两条线段,AB⊥CD,且AB=2,直线AB与平面α所成的角为30°,那么线段CD的取值范围是( )
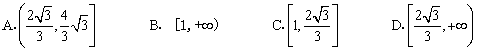
11、已知铜的单晶体的外形是简单几何体,单晶铜有三角形和八边形两种晶面,如果铜的单晶体有24个顶点,每个顶点处都有三条棱,则单晶铜的两种晶面三角形和八边形的数目各为( )
A.6,8 B.8,6
C.6,6 D.8,8
12、已知正方体ABCD—A1B1C1D1的棱长为1,点M在棱AB上,且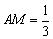 ,点P是平面ABCD内的动点,且点P到直线—A1D1的距离与点P到点M的距离的平方差为1,则点P的轨迹为( ) ,点P是平面ABCD内的动点,且点P到直线—A1D1的距离与点P到点M的距离的平方差为1,则点P的轨迹为( )
A.抛物线 B.双曲线
C.直线 D.以上都不对
第Ⅱ卷(非选择题,共90分)
二、填空题(本题共4个小题,每小题4分,共16分,把正确答案填在题中横线上.)
13、P是二面角α—AB—β棱AB上的一点,分别在α,β上引射线PM,PN,如果∠BPM=∠BPN=45°,∠MPN=60°,那么二面角α—AB—β的大小是______.
[答案]
14、正三棱锥的三条侧棱两两垂直,它的底面积为Q,则它的侧面积为________.
[答案]
15、湖面上浮着一个球,湖水结冰后将球取出,冰上留下一个直径为面24cm,深为8cm的空穴,则此球的半径为________.
[答案]
16、α,β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:
①m⊥n ②α⊥β ③n⊥β ④m⊥α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题______.
[答案]
三、解答题(本大题共6小题,前5小题每小题12分,最后1小题14分,共74分,解答应写出必要的文字说明,证明过程或演算步骤.)
17、已知平面,α,β相交于直线c,而异面直线a,b分别在平面α,β内.求证:
(1)直线a,b至少有一条与c相交;
(2)若a与c相交,而b∥c,则直线b与平面α的距离等于异面直线a,b间的距离.
[答案]
18、三棱锥V—ABC中,AH⊥侧面VBC,且H是△VBC的垂心.
(1)求证:VC⊥AB;
(2)若二面角H—AB—C的大小为30°,求VC与平面ABC所成角的大小.
[答案]
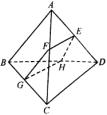
19、如图,在四面体ABCD中,截面EFGH平行于对棱AB和CD.试问:截面在什么位置时,其截面EFGH的面积最大?
[答案]
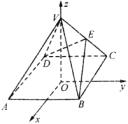
20、如图,以正四棱锥V—ABCD底面中心O为坐标原点建立直角坐标系O—xyz,其中Ox∥BC,Oy∥AB,E为VC的中点,正四棱锥底面边长为2a,高为h.
(1)求 ; ;
(2)设角∠BCV为α,∠DCV为β,且∠BED是二面角α—VC—β的平面角,求∠BED.
[答案]
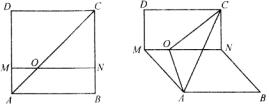
21、四边形ABCD是边长为a的正方形,M、N分别是DA,BC上的点,MN∥AB,MN交AC于O,沿MN折成二面角AB—MN—CD.
(1)求证:不论MN怎样平行移动,∠AOC的大小不变;
(2)MN在什么位置时,AC与MN的距离最大,求出最大值.
[答案]
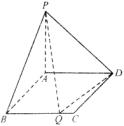
22、如图,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1.
(1)在BC边上是否存在点Q,使PQ⊥QD,说明理由;
(2)若BC边上有且仅有一个点Q,使PQ⊥QD,求AD与平面PDQ所成角的大小;
(3)在(2)的条件下,求平面PQD与平面PAB所成角的大小.
[答案]
|