如何利用直线方程的几种形式和题设的已知条件求直线方程．
若已知直线过定点可设直线方程为点斜式，已知直线的斜率可设直线方程为斜截式，已知直线与截距有关可设直线方程为截距式，其它情况可设直线方程为一般式，再通过待定系数法可求得直线方程．
例1 、已知直线过点P（4，-3），且在坐标轴上的截距的绝对值相等，求直线方程．
分析一： 已知直线上一点，可用点斜式设方程
解答：设直线方程为y+3=k(x-4)，
令 x=0， 有y=-3-4k
令y=0， 有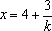 
，
由题意有：
∴k(4k+3)=±(4k+3)
∴k1=1，k2=-1，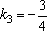
故所求直线方程为：
x+y-1=0， x-y-7=0， 3x+4y=0
分析二： 题中要用到坐标轴上的截距，设截距式．
解答：设直线方程为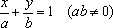
，
∴ 
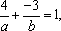又|a|=|b|，
∴ a=b=1或a=7， b=-7．
此时直线方程为 x+y=1，或x-y=7．
又a=b=0时，直线的方程为 3x+4y=0．
综上有，满足条件的直线有三条，为x+y-1=0或x-y-7=0或3x+4y=0．
例2、把函数x=f(x)在x=a及x=b之间的一段图象近似地看作直线，并设a≤c≤b，求证f(c)的近似值是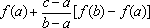
.
解析：设函数y=f(x)的图象上两点A、B的坐标分别为（a，f(a)），（b，f(b)）.由两点式得直线AB的方程为
在y=f(x)的图象上任取一点P（c，f（c））（c∈[a,b]），因为y=f(x)的图象可以近似地看作直线，所以将点P的坐标代入方程①，得：
.
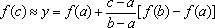如果c=a或c=b，上式仍成立.
例3、光线从点A（－3，4）射出，经x轴上的点B反射后交y轴于C点，再经C点从y轴上反射恰好经过点D（－1，6），求直线AB，BC，CD的方程.
解析：如图所示，作点A关于x轴的对称点，A′（－3，－4），D点关于y轴的对称点D′（1，6），由两点式得直线A′D′（即直线BC）的方程为：
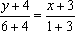，即5x－2y＋7=0.
令y=0，得x=－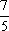
，即B（－
，0），同理可求得C（0，
）.
于是可求得直线AB的方程为5x＋2y＋7=0，
CD的方程为5x＋2y－7=0.
例4、（1）求证：不论m取何实数，直线(2m－1)x－(m＋3)y－(m－11)=0恒过定点，并求此定点坐标.
（2）设二次方程3x2＋2xy－y2＋7x－5y＋k=0表示两条直线，①求k的值；②求两直线方程.
解析：（1）原方程可化为：
（x＋3y－11）－m（2x－y－1）=0
要使直线恒过定点等价于当m∈R时方程恒成立.
∴ 直线恒过定点（2，3）.
（2）方法一：
①将方程变形为3x2＋(2y＋7)x－(y2＋5y－k)=0
∵ 方程表示两条直线
∴ △=16y2＋88y＋(49－12k)为y的完全平方式
∴ 方程16y2＋88y＋49－12k=0的判别式
△′=882－4×16×(49－12k)=0
解得k=－6.
② 当k=－6时，△=16y2＋88y＋121=(4y＋11)2.
∴ ①中关于x的一元二次方程的解为
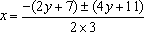
这样原方程表示两条直线
3x－y－2=0及x＋y＋3=0．
方法二：
由题意可设
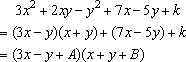
展开右边由待定系数法有
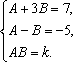解得
∴ 直线方程为x＋y＋3=0和3x－y－2=0.
点评：（1）解决直线系恒过定点的问题常常是把字母看做参数处理.
（2）若二次方程表示两条直线，这说明方程能分解为两个一次因式积的形成．常用的方法是判别式或待定系数法．
