直线的斜率与倾斜角的计算,直线方程的多种形式以及方程与直线斜率、截距之间的关系,要能熟练的进行转化.在解相关问题时,要注意斜率存在的条件,倾斜角的范围,零截距.在直线的方程的各种形式中,要注意相应的约束与限制.
例1: 下列四个命题中的真命题是( )
A、经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示
B、经过任意两个不同的点P1(x1,y1)和P2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示
C、不经过原点的直线都可以用方程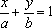 表示
表示
D、经过定点A(0,b)的直线都可以用方程y=kx+b表示.
分析:直线方程的四种形式有不同的限制,与斜率相关则要求斜率存在,应用截距则要求截距存在,而且截距式要求截距不为零.
解答:A中的方程不可以表示垂直于x轴的直线x=x0,C中用截距式不能表示平行于坐标轴的直线,D中也不能表示斜率不存在的直线,B正确.
例2:(全国·文)已知点P到两个定点M(-1,0),N(1,0)的距离的比为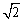 ,点N到直线PM的距离为l,求直线PN的方程.
,点N到直线PM的距离为l,求直线PN的方程.
解析:设点P的坐标为(x,y),由题设有: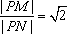 .
.
即: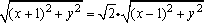 .
.
整理,得x2+y2-6x+1=0①
因为点N到PM的距离为1,|MN|=2,所以∠PMN=30°,直线PM的斜率为±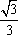 ,直线PM的方程为y=±
,直线PM的方程为y=±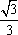 (x+1)②
(x+1)②
将②代入①,并整理得:x2-4x+1=0
∴ x=2+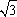 ,x=2-
,x=2-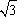 ,代入②式,得P点坐标为(2+
,代入②式,得P点坐标为(2+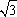 ,1+
,1+ )或(2-
)或(2-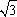 ,-1+
,-1+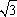 );(2+
);(2+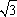 ,-1-
,-1- )或(2-
)或(2-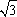 ,1-
,1- ).
).
直线PN的方程为:y=x-1或y=-x+1.
例3:(上海·春招)若直线l的倾斜角为π+arctan(-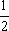 ),且过点(1,0)则直线l的方程为__________.
),且过点(1,0)则直线l的方程为__________.
解析:∵ 直线l的倾斜角为π+arctan(-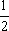 )
)
∴ 直线的斜率为π+tan[arctan(-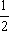 )]=-
)]=-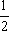
由点斜式可得直线l的方程为y-0=-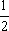 (x-1)即:x+2y-1=0.
(x-1)即:x+2y-1=0.
答案:x+2y-1=0.