又MP∥B1D1,∴ 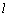 ⊥MP.
⊥MP.
同理,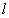 ⊥NP,MP∩NP=P,∴
⊥NP,MP∩NP=P,∴ 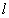 ⊥面MNP.
⊥面MNP.
设Q是所在棱的中点,在图(2),图(3)中,要证明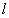 ⊥面MNP不可能,可用反证法证明
⊥面MNP不可能,可用反证法证明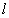 不垂直于面MNP.
不垂直于面MNP.
在图(2)中,若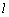 ⊥面MNP,则
⊥面MNP,则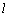 ⊥MN,又
⊥MN,又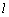 ⊥MQ,
⊥MQ,
∴ 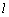 ⊥面MNQ,则
⊥面MNQ,则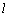 ⊥NQ,即
⊥NQ,即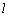 ⊥AD,不可能.
⊥AD,不可能.
在图(3)中,若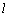 ⊥面MNP,则
⊥面MNP,则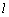 ⊥NP,又
⊥NP,又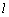 ⊥QN,
⊥QN,
∴ 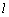 ⊥面NPQ,若
⊥面NPQ,若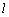 ⊥PQ,即
⊥PQ,即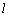 ⊥AB1,也不可能.
⊥AB1,也不可能.
在图(4)中,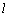 ⊥PQ,
⊥PQ,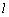 ⊥QN,∴
⊥QN,∴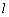 ⊥面PQN,
⊥面PQN,
∴ 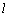 ⊥PN,又
⊥PN,又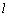 ⊥MP,∴
⊥MP,∴ 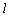 ⊥MNP.
⊥MNP.
有了图(4)中的结论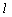 ⊥PN,则在图(5)中必有
⊥PN,则在图(5)中必有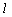 ⊥MN,
⊥MN,
同理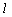 ⊥NP(或
⊥NP(或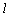 ⊥MP),∴
⊥MP),∴ 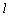 ⊥面MNP.
⊥面MNP.
例2、(全国高考题)如果直线l是平面α的斜线,那么在平面α内( )
A、不存在与l平行的直线
B、不存在与l垂直的直线
C、与l垂直的直线只有一条
D、与l平行的直线有无穷多条
分析:本题是考查直线与平面,直线与直线间的关系.
解答:
由三垂线定理知,在平面α内与l垂直的直线存在,而且在α内所有垂直于l在α内的射影的直线都与l垂直,所以B、C均不正确.
设l与α交于A(斜足),若在α内存在直线a平行于直线l,则由a和l可确定平面β,由于a与a外的一点A,既在α内又在β内,因而α与β重合,所以l在α内,这和l是α的斜线矛盾.由此可知在α内不存在与l平行的直线.
∴ 应选A.
答案:A