折叠与展开
在立体几何中将平面图形翻折成空间图形,或将空间图形展开成平面图形是一个难点,但只要正确分析折前展后的图形,注意对比,注意它们之间点、线、面的相互位置关系哪些改变,哪些没有改变,然后结合所学知识去求解,则并不很困难.
例1、如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,且AD=CD,将△ADE沿DE折起,使点A到达A′,若A′C=A′B,M为DE中点,求证:A′M⊥平面BCDE.
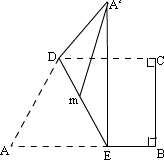
分析:应充分利用“直角”、“等长”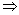 “等腰”,中点等的性质. “等腰”,中点等的性质.
证明:如图,设BC的中点为N,连A′N、MN,A′B,A′C,
则A′M⊥DE,A′N⊥BC,MN⊥BC,
∴ BC⊥平面A′MN,
∴ BC⊥A′M,于是A′M⊥DE,且A′M⊥BC,
又DE与BC相交(否则,∠DEA=90°,AD>AE,与题设AD=AE矛盾),
∴ A′M⊥平面BCDE.
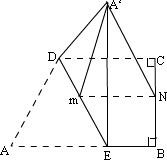
例2、如图,ABCD—A1B1C1D1是一实心长方体木料,且AB=5,AD=4,AA1=3,问一蚂蚁从B点经长方体木料表面爬行到D1的最短距离是多少?
分析:
平面上两点间距离最短,可将木料抽象为一个由几个面围成的几何体,将其沿棱展开成平面图形来解决.
解析:共有如下三种展开方法,可使BD1的连线刚好经过两个表面.
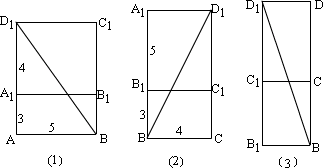
图(1)中有: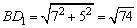
图(2)中有: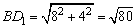
图(3)中有: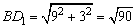
故,蚂蚁爬行的最短路程为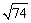 . .
|