本部分内容主要是为后续学习直线与平面所成的角,二面角等概念作铺垫,考题若出现大多以选择和填空题出现,一般试题难度不大,主要考查直线、平面的位置关系.有时利用线线平行关系求异面直线所成的角,这类问题有时有一定的难度和技巧.这些知识都是后续学习简单几何体的基础,因此同学们应该熟练掌握,对这部分内容的练习也是必须的.
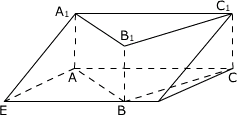
例1、(全国高考试题)如图,已知 A1B1C1-ABC是直三棱柱,过点A1、B、C1的平面和平面ABC的交线记作l,试判定直线A1G1和l的位置关系,并加以证明.
分析:
为了突出考查空间想象力,原题没有画出截面和交线l,并且本题还采用探索性试题的设问,这就对同学们的空间想象力有了更高的要求.其证法既可运用两平面平行性质定理,亦可运用线面平行性质定理.
解答:
证法一:由棱柱定义知平面A1B1C1与平面ABC平行,由题设知直线A1C1=平面A1B1C1∩平面A1BC1,直线l=平面A1BC1∩平面ABC,
根据两平面平行的性质定理有l∥A1C1.
证法二:由棱柱性质,A1C1//AC,
∴ A1C1∥平面ABC,又A1C1 平面A1BC1, 平面A1BC1,
平面A1BC1∩平面ABC=l,
∴由线面平行的性质定理,得 A1C1∥l.
例2、(全国高考试题)如图,已知A1B1C1-ABC是正三棱柱,D是AC中点,证明:AB1∥平面DBC1.

分析:本题考查空间线面关系,充分利用线面平行的判定定理证明.
解答:∵ A1B1C1-ABC是正三棱柱,
∴四边形B1BCC1是矩形.连结B1C交BC1于点E,
则B1E=EC,连结DE.
在△AB1C中,∵ AD=DC,∴ DE∥AB1.
又AB1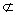 平面DBC1,DE 平面DBC1,DE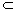 平面DBC1 平面DBC1
∴ AB1∥平面DBC1.
|