直线和平面所成的角,三垂线定理及其逆定理是高考考查的重点,但常与简单几何体综合起来考查,总之,都应熟练掌握.
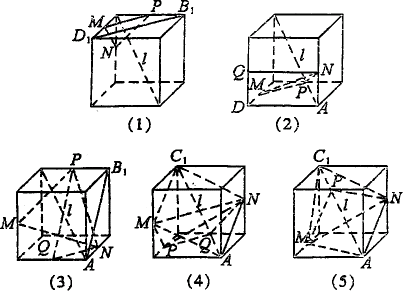
例1、(全国)下列五个正方体图形中,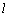 是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出 是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出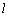 ⊥面MNP的图形的序号是_________.(写出所有符合要求的图形序号) ⊥面MNP的图形的序号是_________.(写出所有符合要求的图形序号)
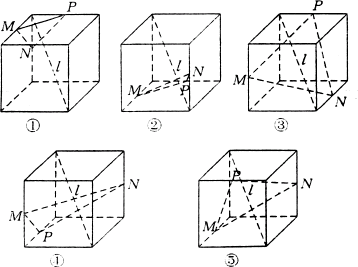
分析:
本题主要考查直线和平面的位置关系,考查空间想象能力和逻辑推理能力,所要用的知识点主要是“由三垂线定理推证,得到的体对角线与其不相交的面对角线垂直”.
解析:
由正方体的对角线与它异面的面对角线垂直,如图(1)中有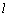 ⊥B1D1, ⊥B1D1,
又MP∥B1D1,∴ 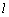 ⊥MP. ⊥MP.
同理,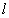 ⊥NP,MP∩NP=P,∴ ⊥NP,MP∩NP=P,∴ 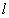 ⊥面MNP. ⊥面MNP.
设Q是所在棱的中点,在图(2),图(3)中,要证明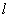 ⊥面MNP不可能,可用反证法证明 ⊥面MNP不可能,可用反证法证明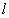 不垂直于面MNP. 不垂直于面MNP.
在图(2)中,若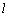 ⊥面MNP,则 ⊥面MNP,则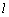 ⊥MN,又 ⊥MN,又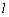 ⊥MQ, ⊥MQ,
∴ 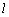 ⊥面MNQ,则 ⊥面MNQ,则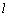 ⊥NQ,即 ⊥NQ,即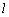 ⊥AD,不可能. ⊥AD,不可能.
在图(3)中,若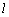 ⊥面MNP,则 ⊥面MNP,则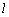 ⊥NP,又 ⊥NP,又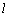 ⊥QN, ⊥QN,
∴ 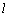 ⊥面NPQ,若 ⊥面NPQ,若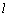 ⊥PQ,即 ⊥PQ,即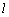 ⊥AB1,也不可能. ⊥AB1,也不可能.
在图(4)中,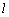 ⊥PQ, ⊥PQ,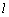 ⊥QN,∴ ⊥QN,∴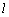 ⊥面PQN, ⊥面PQN,
∴ 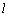 ⊥PN,又 ⊥PN,又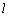 ⊥MP,∴ ⊥MP,∴ 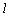 ⊥MNP. ⊥MNP.
有了图(4)中的结论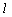 ⊥PN,则在图(5)中必有 ⊥PN,则在图(5)中必有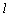 ⊥MN, ⊥MN,
同理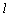 ⊥NP(或 ⊥NP(或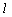 ⊥MP),∴ ⊥MP),∴ 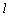 ⊥面MNP. ⊥面MNP.
答案:①④⑤
例2、(全国)如图,已知平行六面体ABCD—A1B1C1D1的底面ABCD是菱形,且∠C1CB =∠C1CD=∠BCD=60°.
(1)证明:C1C⊥BD;
(2)假定CD=2,CC1=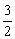 ,记面C1BD为α,面CBD为β,求二面角α—BD—β的平面角的余弦值; ,记面C1BD为α,面CBD为β,求二面角α—BD—β的平面角的余弦值;
(3)当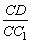 的值为多少时,能使A1C⊥平面C1BD?请给出证明. 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
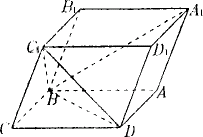
分析:
在高考立体几何题中,证明线线垂直,线面垂直,线面平行,面面平行较为常见,本题第二问我们没学,不讲,对于(1)问可用线面垂直或三垂线定理推线线垂直;对于(3)问,则应考虑到三个角相等,两个面DD1C1C与BB1C1C全等且底面为菱形,从而猜想CD=CC1,证明结论,对于有些类似于此类的问题,我们也常设结论成立,反推条件应如何?
解析:
(1)证法一:如图,连结A1C1、AC,AC和BD交于点O,连结C1O.
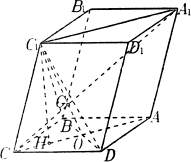
∵ 四边形ABCD是菱形,∴ AC⊥BD,BC=CD.
又∵ ∠BCC1=∠DCC1,C1C=C1C,
∴ △C1BC≌△C1DC.
∴ C1B=C1D.
∵ DO=OB,∴ C1O⊥BD.
但AC⊥BD,AC∩C1O=O,∴ BD⊥平面AC1.
又CC1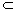 平面AC1.∴ C1C⊥BD. 平面AC1.∴ C1C⊥BD.
证法二:如图.
∵ ∠C1CB=∠C1CD,
∴ C1C在平面AC上的射影CH为∠BCD的平分线.
∵ 底面ABCD为菱形,∴ C1C在平面AC上的射影为AC.
∵ AC⊥BD,∴ C1C⊥BD.
(3)证法一:如图所示,不妨设CD=1,C1C=λ>0,
则正ΔBCD中BD上的高OC=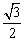 . .
由(1)知BD⊥平面AA1C1C,
∴ 由BD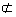 平面C1BD知,平面AA1C1C⊥平面C1BD于OC1. 平面C1BD知,平面AA1C1C⊥平面C1BD于OC1.
∴ 欲使AC1⊥平面C1BD,只需A1C⊥C1O.
设C1O∩A1C=P,则由A1C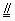 2·C1O,得 2·C1O,得
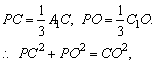
即A1C2+C1O2=9·CO2 ①
又∠C1CB=∠C1CD=∠BCD=60°,易得cos∠C1CO=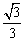 . .
在△C1CO和△A1CA中,有
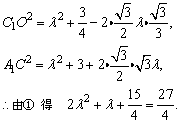
解得λ=1(舍去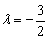 ). ).
故当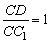 时,能使A1C⊥平面C1BD. 时,能使A1C⊥平面C1BD.
证法二:
由(1)知,BD⊥平面AC1.
∵ A1C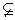 平面AC1,∴ BD⊥A1C. 平面AC1,∴ BD⊥A1C.
当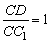 时,平行六面体的六个面是全等的菱形,同BD⊥A1C的证法可得BC1⊥A1C. 时,平行六面体的六个面是全等的菱形,同BD⊥A1C的证法可得BC1⊥A1C.
又BD∩BC1=B,∴ A1C⊥平面C1BD.
|