一道数学试题的拓展
题目:已知异面直线a与b所成的角为50°,P为空间一定点,则过点P且与a、b所成的角都是30°的直线有且仅有( )
A.1条 B.2条 C.3条 D.4条
这是93年一道理科高考试题,要解决这道题目,首先要证明一个预备定理.
预备定理:平面的一条斜线和平面内经过斜足的直线所成的角大于斜线在这个平面内的射影与这条直线所成的锐角.
下面来证明这个定理.
已知:如图,PO是平面α的斜线,O是斜足,PA⊥α于A,BO是α内过点O的直线,若∠POB是锐角.
求证:∠POB>∠AOB.
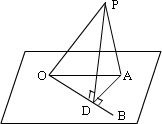
证明:若OB与OA重合,则∠AOB=0°,显然有∠POB>∠AOB,
下证OB不与OA重合的情形
过A作AD⊥OB于D,连PD,由三垂线定理知 PD⊥OB,
∴cos∠POB=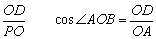 , ,
∵OP>OA,∴cos∠POB< cos∠AOB,
又∵∠POB,∠AOB都是锐角,
∴ POB>∠AOB ,即证.
下面再来看这道试题
解答:过空间一点P作直线a′∥a,b′∥b. 记过a′、b′的平面α,
∵ a、b所成角为50°,
∴a′、b′所成角为50°或130°,显然在α内不存在过点P且与a′、b′都成30°角的直线.
∴若所求直线存在,则必在α外,由课本上的习题结论知此直线的射影必为直线a′、b′所成角的角平分线.
①对于a′、b′所成的50°的角,其角平分线与a′、b′所成角为25°,当过P点的直线从这角平分线的位置沿竖直方向绕点P抬起的过程中,由预备定理知,该直线与a′、b′所成角从25°逐渐增加,必有一位置等于30°,这样的直线有两条,如图

②对于a′、b′所成的130°的角,其角平分线与a′、b′所成的角为65°,而30°<65°,∴不可能有直线与a′、b′所成角为30°.
∴这样的直线只有2条.
拓展:
在该题中,若50°不变,将30°改为25°,则答案为1条,此条直线即为①种情形中a′与b′的角平分线所在直线;若50°不变,将30°改为65°,则答案为3条,即①种情形2条,②种情形1条;若50°不变,将30°改为70°,则答案为4条,①种情形、②种情形各2条;若50°不变,将30°改为20°,则答案为0条;若50°不变,将30°改为90°,则答案为1条.
延伸:空间两条不垂直的异面直线a、b所成的角为α过空间一定点P与a、b所成角都是θ的直线l有多少条?
则答案应为:当θ∈(0, )时, )时, 有0条; 有0条;
当θ=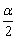 时, 时,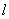 有1条; 有1条;
当θ∈(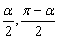 )时, )时,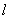 有2条; 有2条;
当θ= 时, 时,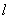 有3条; 有3条;
当θ∈( )时, )时,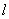 有4条; 有4条;
当θ=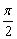 时, 时, 有1条. 有1条.
练习:过空间一点与两条异面直线都成30°角的直线的条数是( )
A.1条 B.2条
C.0条或1条或2条 D.1条或2条或3条或4条
答案:C.
|