|
|
对于空间的角的计算问题,一般以多面体特别是三棱锥、四棱锥、正方体、长方体等为载体,考查点、线、面位置关系,求距离和角度.一般是逐步设问,难度逐步加深.求解空间的角的问题,常见的是异面直线所成的角,直线和平面所成的角,平面与平面所成的角,这类试题有一定的难度和技巧,通常把它们转化成相交直线所成的角,要在练习中注意解决求角的方法.
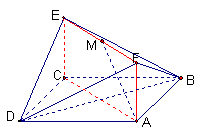
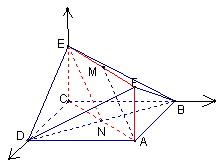
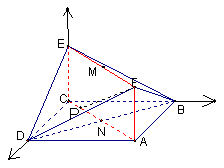
例1、(浙江高考试题)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=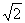 ,AF=1,M是线段EF的中点。 ,AF=1,M是线段EF的中点。
(Ⅰ)求证AM∥平面BDE;
(Ⅱ)求二面角A—DF—B的大小;
(Ⅲ)试在线段AC上确定一点P,使得PF与BC所成的角是60°.
分析:
本题主要考查空间线面关系等基础知识,同时考查空间想象能力和运算能力。特别是利用向量解决线线角、线面角、面面角及点面距离具有一定的优势。
解答:方法一
解: (Ⅰ)记AC与BD的交点为O,连接OE,
∵O、M分别是AC、EF的中点,ACEF是矩形,
∴四边形AOEM是平行四边形,
∴AM∥OE.
∵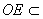 平面BDE, 平面BDE,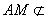 平面BDE, 平面BDE,
∴AM∥平面BDE。
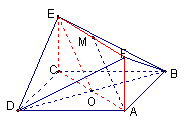 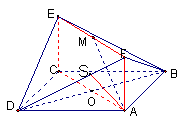
(Ⅱ)在平面AFD中过A作AS⊥DF于S,连结BS,
∵AB⊥AF, AB⊥AD,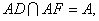
∴AB⊥平面ADF,
∴AS是BS在平面ADF上的射影,
由三垂线定理得BS⊥DF。
∴∠BSA是二面角A—DF—B的平面角。
在RtΔASB中,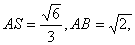
∴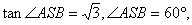
∴二面角A—DF—B的大小为60°。
(Ⅲ)设CP=t(0≤t≤2),作PQ⊥AB于Q,则PQ∥AD,
∵PQ⊥AB,PQ⊥AF,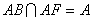 , ,
∴PQ⊥平面ABF,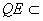 平面ABF, 平面ABF,
∴PQ⊥QF。
在RtΔPQF中,∠FPQ=60°,
PF=2PQ。
∵ΔPAQ为等腰直角三角形,
∴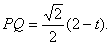
又∵ΔPAF为直角三角形,
∴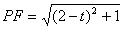 , ,
∴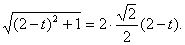
所以t=1或t=3(舍去)
即点P是AC的中点。
方法二
(Ⅰ)建立如图所示的空间直角坐标系。
设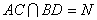 ,连接NE, ,连接NE,
则点N、E的坐标分别是(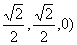 、(0,0,1), 、(0,0,1),
∴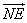 =( =(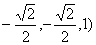 , ,
又点A、M的坐标分别是(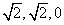 )、( )、(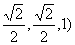 , ,
∴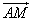 =( =(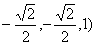
∴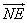 = =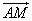 且NE与AM不共线,∴NE∥AM。 且NE与AM不共线,∴NE∥AM。
又∵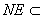 平面BDE, 平面BDE,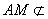 平面BDE, 平面BDE,
∴AM∥平面BDF。
(Ⅱ)∵AF⊥AB,AB⊥AD,AF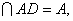 ∴AB⊥平面ADF。 ∴AB⊥平面ADF。
∴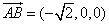 为平面DAF的法向量。 为平面DAF的法向量。
∵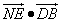 =( =(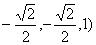 · ·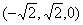 =0, =0,
∴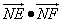 =( =(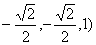 · ·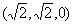 =0得 =0得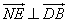 , ,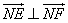 , ,
∴NE为平面BDF的法向量。
∴cos<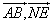 >= >=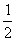
∴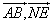 的夹角是60°。 的夹角是60°。
即所求二面角A—DF—B的大小是60°。
(Ⅲ)设P(t,t,0)(0≤t≤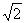 )得 )得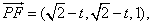
∴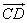 =( =(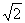 ,0,0) ,0,0)
又∵PF和CD所成的角是60°。
∴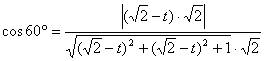
解得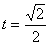 或 或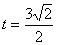 (舍去),即点P是AC的中点。 (舍去),即点P是AC的中点。
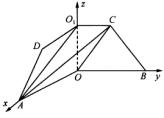
例2、(湖南省)如图,已知ABCD是上、下底边长分别为2和6,高为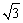 的等腰梯形,将它沿对称轴OO1折成直二面角,如图. 的等腰梯形,将它沿对称轴OO1折成直二面角,如图.
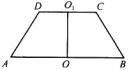 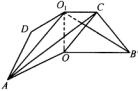
(1)证明:AC⊥BO1;
(2)求二面角O—AC—O1的大小.
分析:
本题考查直线和直线,直线和平面的位置关系,异面直线所成的角,二面角等基本知识,以及空间想象能力和逻辑推理能力.
解答:
(1)证明:由题设知OA⊥OO1,OB⊥OO1,所以∠AOB是所折成的直二面角的平面角,即OA⊥OB.故可以O为原点,OA、OB、OO1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则相关各点的坐标是A(3,0,0),B(0,3,0),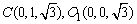 . .
从而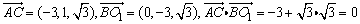 . .
所以AC⊥BO1;
(2)解:因为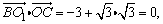 所以BO1⊥OC, 所以BO1⊥OC,
再由(1)AC⊥BO1,所以BO1⊥平面OAC,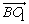 是平面OAC的一个法向量. 是平面OAC的一个法向量.
再设n=(x,y,z)是平面O1AC的一个法向量,
由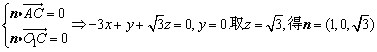 . .
设二面角O—AC—O1的大小为θ,由n、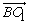 的方向可知 的方向可知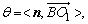
所以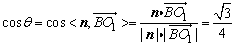
即二面角O—AC—O1的大小是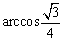 . .
|
|
|
|