带电粒子在磁场(或加有电场、重力场的复合场)中的运动是高考命题的热点。考题一般综合性强,多把电场的性质,运动学规律、牛顿运动定律、圆周运动知识、功能关系等有机结合在一起,难度为中等以上,对考生的物理过程和运动规律的综合分析能力,空间想象能力、运用数学工具解决物理问题的能力都有较高的要求。同学们在学习中要多下功夫。
例1、如图所示,虚线MN是垂直纸面的平面与纸面的交线,在平面右侧的半空间存在一磁感强度为B的匀强磁场,方向垂直纸面向外。O是MN上的一点,从O点可以向磁场区域发射电量为+q、质量为m、速率为v的粒子。粒子射入磁场时的速度可在纸面和各个方向。已知先后射入的两个粒子恰好在磁场中给定的P点相遇,P到O的距离为L,不计重力及粒子间的相互作用。
(1)求所考查的粒子在磁场中的轨道半径
(2)求这两个粒子从O点射入磁场的时间间隔。
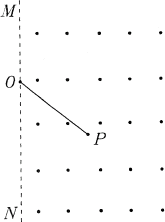
解析:
(1)设粒子在磁场中做圆周运动的轨道半径为R,由牛顿第二定律,有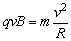 。 。
∴ 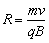
(2)如图所示,以OP为弦可画出两个半径相同的圆,分别表示在P点相遇的两个粒子的轨道,圆心和直径分别是O1、O2和OO1Q1、OO2Q2,在O处两个圆的切线分别表示两个粒子的射入方向,用θ表示它们这间的夹角,由几何关系可知∠PO1Q1=∠PO2Q2=θ.

从O点射入到相遇,粒子1的路程为半个圆周加弧长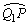 。 。
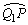 =Rθ. =Rθ.
粒子2的路程为半个圆周减去弧长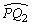 。 。
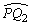 =Rθ. =Rθ.
粒子1的运动时间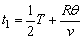 , ,
其中T为圆周运动的周期。
粒子2的运动时间为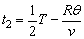 。 。
两粒子射入的时间间隔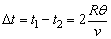 。 。
因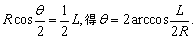
由以上可得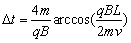 。 。
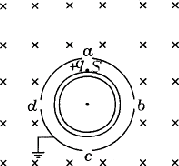
例2、如图所示,两个共轴的圆筒形金属电极,外电极接地,其上均匀分布着平行于轴线的四条狭缝a、b、c和d,外筒的外半径为r0,在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场,磁感强度的大小为B。在两极间加上电压,使两圆筒之间的区域内有沿半径向外的电场。一质量为m,带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零,如果该粒子经过一段时间的运动之后恰好又回到出发点S,则两电极之间的电压U应是多少?(不计重力,整个装置在真空中)。
精析:
如图所示,带电粒子从S出发,在两筒之间的电场力作用下加速,沿径向穿出a而进入磁场区,在洛伦兹力作用下做匀速圆周运动。粒子再回到S点的条件是能沿径向穿过狭缝d,只要穿过了d,粒子就会在电场力作用下先减速,再反向加速,经d重新进入磁场区,然后,粒子将以同样方式经过c、b,再经过a回到S点。设粒子射入磁场区的速度为v,根据能量守恒,有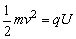 。 。
设粒子在洛伦兹力作用下做匀速圆周运动的半径为R,由洛伦兹力公式和牛顿定律得: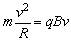 。 。
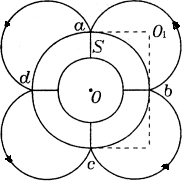
由前面分析可知,要回到S点,粒子从a到d必经过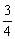 圆周,所以半径R必定等于筒的外半径r0,即R=r0。 圆周,所以半径R必定等于筒的外半径r0,即R=r0。
由以上各式解得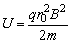 。 。
例3、电视机的显像管中,电子束的偏转是用磁偏转技术实现的。电子束经过电压为U的加速电场后,进入一圆形匀强磁场区,如图所示。磁场方向垂直于圆面。磁场区的中心为O,半径为r。当不加磁场时,电子束将通过O点而打到屏幕的中心M点。为了让电子束射到屏幕边缘P,需要加磁场,使电子束偏转一已知角度θ,此时磁场的磁感应强度B应为多少?

精析:
电子在磁场中沿圆弧ab运动,圆心为C,半径为R,以v表示电子进入磁场时的速度,m、e分别表示电子的质量和电量,则: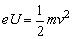 。 。
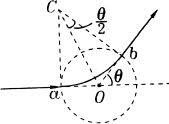
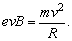
又有 , ,
由以上各式解得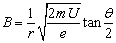 。 。
|